题目内容
如图，A、B、C是⊙O上三点，且C是
的中点，连接OA、OB．
（1）如图1，若∠AOB=120°，求证：四边形OACB是菱形，并求
的值．
（2）如图2，弦CD⊥OA于点E，若sin∠CDB=
，求tan∠DBC的值．
 |
| AB |
（1）如图1，若∠AOB=120°，求证：四边形OACB是菱形，并求
| AB |
| OC |
（2）如图2，弦CD⊥OA于点E，若sin∠CDB=
| 1 |
| 3 |
考点：菱形的判定,垂径定理,圆心角、弧、弦的关系,解直角三角形
专题：
分析：（1）利用等边三角形的性质得出AC=OA=OB=BC，再利用菱形的判定得出即可，由
=
，得出
的值．
（2）首先构造直角三角形，求出FB以及FO的长，再利用垂径定理以及圆周角定理得出∠CBD=∠AOC=∠COB，进而得出答案．
| AM |
| AO |
| ||
| 2 |
| AB |
| OC |
（2）首先构造直角三角形，求出FB以及FO的长，再利用垂径定理以及圆周角定理得出∠CBD=∠AOC=∠COB，进而得出答案．
解答：（1）证明：∵C是弧BC的中点，∠AOB=l20°
∴∠AOC=∠BOC=60°，
又∵OA=OC=OB，
∴△OAC和△OBC都是等边三角形，
∴AC=OA=OB=BC，
∴四边形OACB是菱形．
∵∠AOC=60°，
∴
=
，
∴AM=
AO，
∴AB=
AO，
∵CO=AO，
∴
=
；
（2）解：连接CO并延长交⊙O于点M，连接BM，过点B作BF⊥CM于点F，
∵∠CDB=∠CMB，sin∠CDB=
，
∴sin∠CMB=
=
，
设BC=x，则MC=3x，
故BM=2
x，
∴BF•MC=BC•BM，
∴BF=
=
x，
∴FO=
=
x，
∴tan∠FOB=
=
=
，
∵C是
的中点，
∴∠AOC=∠COB，
∵弦CD⊥OA于点E，
∴
=
，
∴∠CBD=∠AOC=∠COB，
∴tan∠DBC=
．
∴∠AOC=∠BOC=60°，
又∵OA=OC=OB，
∴△OAC和△OBC都是等边三角形，
∴AC=OA=OB=BC，
∴四边形OACB是菱形．
∵∠AOC=60°，
∴
| AM |
| AO |
| ||
| 2 |
∴AM=
| ||
| 2 |
∴AB=
| 3 |
∵CO=AO，
∴
| AB |
| OC |
| 3 |
（2）解：连接CO并延长交⊙O于点M，连接BM，过点B作BF⊥CM于点F，
∵∠CDB=∠CMB，sin∠CDB=
| 1 |
| 3 |
∴sin∠CMB=
| BC |
| CM |
| 1 |
| 3 |
设BC=x，则MC=3x，
故BM=2
| 2 |
∴BF•MC=BC•BM，
∴BF=
x•2
| ||
| 3x |
2
| ||
| 3 |
∴FO=
| BO2-BF2 |
| 7 |
| 6 |
∴tan∠FOB=
| BF |
| FO |
| ||||
|
4
| ||
| 7 |
∵C是
|
| AB |
∴∠AOC=∠COB，
∵弦CD⊥OA于点E，
∴
|
| AC |
|
| AD |
∴∠CBD=∠AOC=∠COB，
∴tan∠DBC=
4
| ||
| 7 |
点评：此题主要考查了菱形的判定以及圆周角定理以及其推论和勾股定理的等知识，用同一未知数表示出BF，FO的长是解题关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P．在新图形中你发现了什么？请写出一条；在若点P的坐标为（2a，b+1），则a与b的数量关系为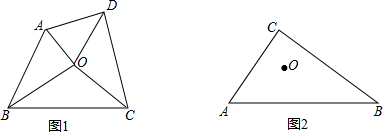
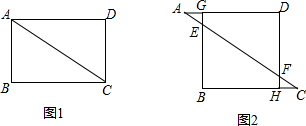
在已建立直角坐标系的4×4正方形方格纸中，若每个小正方形的边长为1，在4×4方格纸中平移一次线段BC后的像为AD，以A，B，C，D为顶点的四边形是菱形，
如图，AB是⊙O的直径，AB垂直于弦CD，∠BOC=70°，则∠ABD=