题目内容
17.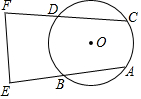 如图,已知在⊙O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF,求证:EF的垂直平分线经过点O.
如图,已知在⊙O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF,求证:EF的垂直平分线经过点O.
分析 过点O作OG⊥CF于点G,OH⊥AE于点H,由垂径定理和勾股定理可知OH=OG,OE=OF,然后利用勾股定理证明OE=OF,由等腰三角形的性质可知EF的垂直平分线必过O点.
解答 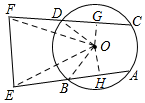 解:过点O作OG⊥CF于点G,OH⊥AE于点H,连接OF、OE,
解:过点O作OG⊥CF于点G,OH⊥AE于点H,连接OF、OE,
∴由垂径定理可知:BH=$\frac{1}{2}$AB,DG=$\frac{1}{2}$CD,
∵AB=CD,
∴BH=DG,
∵OD=OB,
∴由勾股定理可知:OG2=OH2,
∵BE=DF,
∴BE+BH=DF+DG,
∴EH=FG,
∴在Rt△OEH与Rt△OFG中,
由勾股定理可知:OE2=OF2,
∴OE=OF,
∴△OFE是等腰三角形,
∴由等腰三角形的三线合一可知:EF的垂直平分线过O点.
点评 本题考查垂径定理,涉及勾股定理,等腰三角形的性质,解题的关键是证明△OEF是等腰三角形,然后利用三线合一说明EF的垂直平分线经过点O,本题属于基础题型.

练习册系列答案
相关题目
7.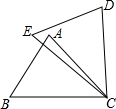 如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
 如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )| A. | ∠BCE=∠ACD | B. | AC=DC | C. | ∠A=∠D | D. | AB=DE |
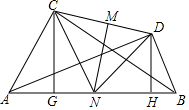 已知:如图,∠ACB=∠ADB=90°,M、N分别是CD、AB的中点,连结CN、DN,过点C作CG⊥AB,过点D作DH⊥AB,恰好有CG=NH.
已知:如图,∠ACB=∠ADB=90°,M、N分别是CD、AB的中点,连结CN、DN,过点C作CG⊥AB,过点D作DH⊥AB,恰好有CG=NH.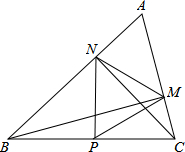 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM.PN.
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM.PN. 在数轴上作出表示$\sqrt{10}$的点.
在数轴上作出表示$\sqrt{10}$的点.