题目内容
9．关于x的分式方程$\frac{2m+x}{x-3}$-1=$\frac{2}{x}$有增根，请求出增根及此时m的值．分析 分式方程去分母转化为整式方程，由分式方程有增根，求出x的值，代入整式方程求出m的值即可．
解答 解：原方程去分母得：（2m-5）x=-6，
根据原方程有增根，得到x（x-3）=0，
解得：x=0或x=3，
当x=0时，m不存在；
当x=3时，m=-$\frac{3}{2}$．
点评 此题考查了分式方程的增根，增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
如图，直线l同侧有A、B两点，请利用直尺和圆规在直线l上求作一点P，使AP+BP值最小．（不写作法，保留作图痕迹）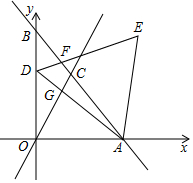
如图，已知一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象与x轴、y轴分别交于A、B两点，与正比例函数y=$\sqrt{3}$x的图象交于点C，点D是线段OB上的一个动点（不包含O、B两点），以AD为边在其一侧作等边三角形ADE，DE交AB于F，AD交OC于G．
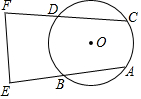如图，已知在⊙O中，弦AB=CD，延长AB到E，延长CD到F，使BE=DF，求证：EF的垂直平分线经过点O．
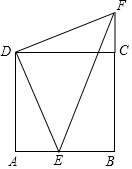已知：如图，E点是正方形ABCD的边AB上一点，AB=4，DE=6，△DAE逆时针旋转后能够与△DCF重合．
19．某自行车厂一周计划生产1400辆自行车，平均每天生产自行车200辆，由于各种原因，实际每天生产量与计划每天生产量相比有出入．下表是某周的自行车生产情况（超计划生产量为正、不足计划生产量为负，单位：辆）
（1）根据记录可知前三天共生产自行车599辆；产量最多的一天比产量最少的一天多生产26辆；
（2）若该厂实行按生产的自行车数量的多少计工资，即计件工资制．如果每生产一辆自行车可得人民币60元，那么该厂工作这一周的工资总额是多少元？
（3）为了提高工作的积极性，工厂决定对超出任务量（指计划量）的部分额外奖励15元/车，不足任务量的部分倒扣15元/辆，如果工厂有工人a人，那么该厂工人这一周的人均工资是多少元？（用含a的代数式表示）
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
（2）若该厂实行按生产的自行车数量的多少计工资，即计件工资制．如果每生产一辆自行车可得人民币60元，那么该厂工作这一周的工资总额是多少元？
（3）为了提高工作的积极性，工厂决定对超出任务量（指计划量）的部分额外奖励15元/车，不足任务量的部分倒扣15元/辆，如果工厂有工人a人，那么该厂工人这一周的人均工资是多少元？（用含a的代数式表示）