题目内容
12.已知关于x的一元二次方程(m-1)x2+x+1=0.(1)若方程有两个实数根,求m的取值范围;
(2)当m取最大的整数时,求这个方程的根.
分析 (1)由方程有两个相等的实数根得△=b2-4ac≥0,可得关于m的不等式,解之可得m的范围,结合一元二次方程的定义可得答案;
(2)由(1)知m=0,得出方程,公式法求解可得.
解答 解:(1)∵方程有两个实数根,
∴b2-4ac=1-4×(m-1)×1=5-4m≥0,
解得:m≤$\frac{5}{4}$,
又m-1≠0,即m≠1,
∴m≤$\frac{5}{4}$且m≠1;
(2)当m=0时,方程为-x2+x+1=0,
解得:x=$\frac{1±\sqrt{5}}{2}$.
点评 本题主要考查根的判别式和一元二次方程的定义、解一元二次方程的能力,掌握一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系是解题的关键.

练习册系列答案
相关题目
3.下列函数中是二次函数的是( )
| A. | y=3x-1 | B. | y=x3-2x-3 | C. | y=(x+1)2-x2 | D. | y=3x2-1 |
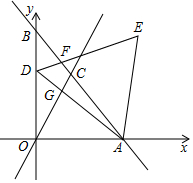 如图,已知一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象与x轴、y轴分别交于A、B两点,与正比例函数y=$\sqrt{3}$x的图象交于点C,点D是线段OB上的一个动点(不包含O、B两点),以AD为边在其一侧作等边三角形ADE,DE交AB于F,AD交OC于G.
如图,已知一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象与x轴、y轴分别交于A、B两点,与正比例函数y=$\sqrt{3}$x的图象交于点C,点D是线段OB上的一个动点(不包含O、B两点),以AD为边在其一侧作等边三角形ADE,DE交AB于F,AD交OC于G.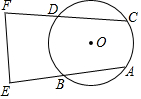 如图,已知在⊙O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF,求证:EF的垂直平分线经过点O.
如图,已知在⊙O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF,求证:EF的垂直平分线经过点O.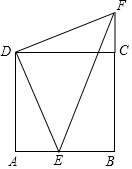 已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.