题目内容
9.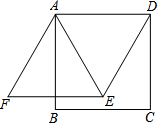 如图,在正方形ABCD中,以AD为边作等边三角形ADE,点E在正方形内部,将AB绕着点A顺时针旋转30°得到线段AF,连结EF.求证:四边形ADEF是菱形.
如图,在正方形ABCD中,以AD为边作等边三角形ADE,点E在正方形内部,将AB绕着点A顺时针旋转30°得到线段AF,连结EF.求证:四边形ADEF是菱形.
分析 首先利用等边三角形的性质可得AD=DE=AE,∠DAE=60°,进而可得∠BAE=30°,再根据将AB绕着点A顺时针旋转30°得到线段AF可得AB=AF,∠BAF=30°,然后可证出△AEF是等边三角形,从而可得AF=EF=DE=AD,再根据四边相等的四边形是菱形可得四边形ADEF是菱形.
解答 证明:如图,
∵△ADE是等边三角形,
∴AD=DE=AE,∠DAE=60°,
∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°,
∴∠BAE=30°.
∵AB=AF,∠BAF=30°,
∴AF=AE,∠EAF=60°.
∴△AEF是等边三角形.
∴AF=EF=DE=AD.
∴四边形ADEF是菱形;
证法二:
证明:如图,
∵△ADE是等边三角形,
∴AD=DE,∠DAE=60°,
∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°,
∴∠BAE=30°,
∵AB=AF,∠BAF=30°,
∴AF=DE,∠EAF=∠AED=60°.
∴AF∥DE,
∴四边形ADEF是平行四边形.
∴AD=DE.
∴平行四边形ADEF是菱形.
点评 此题主要考查了菱形的判定,以及等边三角形的判定与性质,关键是掌握四边相等的四边形是菱形.

练习册系列答案
相关题目
 已知点P为线段AB上一点,射线PM⊥AB,用直尺和圆规在PM上找一点C,使得PC2=AP•PB.
已知点P为线段AB上一点,射线PM⊥AB,用直尺和圆规在PM上找一点C,使得PC2=AP•PB. 在Rt△ABC中,∠C=90°,AC=4,BC=3,现将延长BC到D,使△ABD为等腰三角形,求等腰△ABD的周长.
在Rt△ABC中,∠C=90°,AC=4,BC=3,现将延长BC到D,使△ABD为等腰三角形,求等腰△ABD的周长. 如图,在平面直角坐标系中,点A(m,2)在第一象限.若点A关于y轴的对称点B在反比例函数$y=-\frac{6}{x}$的图象上,则m的值为( )
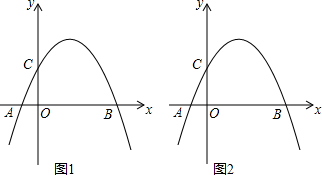
如图,在平面直角坐标系中,点A(m,2)在第一象限.若点A关于y轴的对称点B在反比例函数$y=-\frac{6}{x}$的图象上,则m的值为( ) 已知二次函数的图象与x轴的交点坐标为(3,0)和(-1,0),且经过点(1,-4),
已知二次函数的图象与x轴的交点坐标为(3,0)和(-1,0),且经过点(1,-4),