题目内容
17. 在Rt△ABC中,∠C=90°,AC=4,BC=3,现将延长BC到D,使△ABD为等腰三角形,求等腰△ABD的周长.
在Rt△ABC中,∠C=90°,AC=4,BC=3,现将延长BC到D,使△ABD为等腰三角形,求等腰△ABD的周长.
分析 分三种情况讨论:①如图1,当AB=AD=5时,CD=CB=3,得△ABD的周长为16m;②如图2,当AB=BD=5时得CD=2,在Rt△ACD中,AD=$\sqrt{{AC}^{2}{+CD}^{2}}$=2,得到△ABD的周长=10+2$\sqrt{5}$;③如图3当AB为底时.则设腰AD=BD=x,则CD=x-3,在Rt△ACD中,由勾股定理得x2=(x-3)2+42,解得:x=$\frac{25}{6}$,得到△ABD的周长为$\frac{40}{3}$m.
解答 解:在Rt△ABC中,AB=$\sqrt{{AC}^{2}{+BC}^{2}}$=5,
①如图1,
当AB=AD=5时,
CD=CB=3,
得△ABD的周长为16m;
②如图2,
当AB=BD=5时,
得CD=2,
在Rt△ACD中,AD=$\sqrt{{AC}^{2}{+CD}^{2}}$=2$\sqrt{5}$
∴△ABD的周长=10+2$\sqrt{5}$;
③如图3,
当AB为底时,设AD=BD=x,则CD=x-3,
在Rt△ACD中,AD2=CD2+AC2,
即x2=(x-3)2+42,解得:x=$\frac{25}{6}$,
则△ABD的周长为$\frac{40}{3}$m.
点评 本题考查了勾股定理,解决本题的关键是正确认识到需要讨论,讨论等腰三角形的边应如何分类.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
2.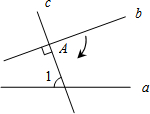 如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
 如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )| A. | 70° | B. | 50° | C. | 30° | D. | 20° |
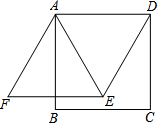 如图,在正方形ABCD中,以AD为边作等边三角形ADE,点E在正方形内部,将AB绕着点A顺时针旋转30°得到线段AF,连结EF.求证:四边形ADEF是菱形.
如图,在正方形ABCD中,以AD为边作等边三角形ADE,点E在正方形内部,将AB绕着点A顺时针旋转30°得到线段AF,连结EF.求证:四边形ADEF是菱形.