题目内容
12．
如图，在△ABC中，∠ABC=90°，BD为AC边上的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若AG=13，BG=5，则CF的长为6．
分析 首先可判断四边形BGFD是平行四边形，再由直角三角形斜边中线等于斜边一半，可得BD=FD，则可判断四边形BGFD是菱形，则GF=5，则AF=8，AC=10，在Rt△ACF中利用勾股定理可求出CF的值．
解答 解：∵AG∥BD，BD=FG，
∴四边形BGFD是平行四边形，
∵CF⊥BD，
∴CF⊥AG，
又∵点D是AC中点，
∴BD=DF=$\frac{1}{2}$AC，
∴四边形BGFD是菱形，
∴GF=BG=5，则AF=13-5=8，AC=2×5=10，
∵在Rt△ACF中，∠CFA=90°，
∴AF2+CF2=AC2，即82+CF2=102，
解得：CF=6．
故答案是：6．
点评 本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质，解答本题的关键是判断出四边形BGFD是菱形．
练习册系列答案
相关题目
2．
如图，将四根长度相等的木条首尾相连，钉成四边形ABCD，并转动四边形ABCD使其形状改变，当∠A=60°，测得BD=1，则当∠A=90°时，BD长为（ ）
如图，将四根长度相等的木条首尾相连，钉成四边形ABCD，并转动四边形ABCD使其形状改变，当∠A=60°，测得BD=1，则当∠A=90°时，BD长为（ ）| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
有一长32厘米，宽14厘米的铁皮，若要用该铁皮做一个底面积为180平方厘米的有盖盒子，则盒子的高应为多少？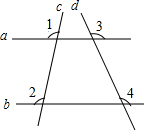
如图，直线a，b与直线c，d相交，已知∠1=∠2，∠3=110°，则∠4的度数为110°．
如图，AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB=1，CD=3，则EF：CD的值为$\frac{1}{4}$．
1．
如图，在△ABC中，AB=AC，AE是经过点A的一条直线，且B、C在AE的两侧，BD⊥AE于D，CE⊥AE于E，AD=CE，则∠BAC的度数是（ ）
如图，在△ABC中，AB=AC，AE是经过点A的一条直线，且B、C在AE的两侧，BD⊥AE于D，CE⊥AE于E，AD=CE，则∠BAC的度数是（ ）| A． | 45° | B． | 60° | C． | 90° | D． | 120° |