Question

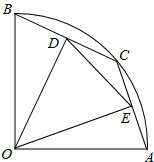
如图，AB为⊙O的直径，CB⊥AB，连接OC过A作AD∥OC交⊙O于D，连接CD并延长交BA的延长线于E．
（1）求证：CD是⊙O的切线；
（2）若AE=1，DE=2，求AB的长．

Answer 1

考点：切线的判定,全等三角形的判定与性质,勾股定理

专题：

分析：（1）先利用SAS证明△COD≌△COB，然后由全等三角形的对应角相等，求得∠CDO=90°，即可证得直线CD是⊙O的切线；
（2）设OA=OD=x，在Rt△EDO中，根据勾股定理得出ED²+OD²=EO²，据此列出方程2²+x²=（x+1）²，解方程求出x=

3

2

，进而得出AB=2AO=3．

解答：（1）证明：∵OB、OD为⊙O的半径，
∴OB=OD，
∴∠OAD=∠ODA．
∵AD∥OC，
∴∠OAD=∠COB，∠ODA=∠COD，
∴∠COD=∠COB．
在△CDO和△CBO中，

OD=OB ∠COD=∠COB CO=CO

，
∴△COD≌△COB（SAS），
∴∠CDO=∠CBO=90°，
∴OD⊥CD，
∴CD是⊙O的切线；

（2）解：设OA=OD=x．
在Rt△EDO中，ED²+OD²=EO²，
∴2²+x²=（x+1）²，
解得：x=

3

2

，
∴AB=2AO=3，
∴AB的长为3．

点评：此题考查了切线的判定、全等三角形的判定与性质以及勾股定理．此题难度适中，注意数形结合与方程思想的应用．