题目内容
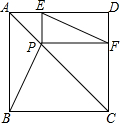 如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足,
如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足,(1)求证:四边形EPFD为矩形;
(2)求证:BP=EF;
(3)过E,P,F三点作⊙O,设正方形ABCD的边长为4,当AC与⊙O相切时,求BP的长.
考点:正方形的性质,全等三角形的判定与性质,矩形的判定,切线的性质
专题:
分析:(1)根据正方形的性质可得∠D=90°,再根据垂直的定义求出∠PED=∠PFD=90°,然后根据四个角都相等的四边形是矩形证明即可;
(2)连接PD,根据正方形的性质可得∠BAP=∠DAP,AB=AD,然后利用“边角边”证明△ABP和△ADP全等,根据全等三角形对应边相等可得BP=DP,再根据矩形的对角线相等可得DP=EF,从而得证;
(3)设DP、EF的交点为O,根据矩形的对角线互相平分且相等可得点O到E、P、F、D的距离相等,从而判断出PD、EF为⊙O的直径,再根据直线与圆相切的定义可得PD⊥AC,然后根据正方形的性质求解即可.
(2)连接PD,根据正方形的性质可得∠BAP=∠DAP,AB=AD,然后利用“边角边”证明△ABP和△ADP全等,根据全等三角形对应边相等可得BP=DP,再根据矩形的对角线相等可得DP=EF,从而得证;
(3)设DP、EF的交点为O,根据矩形的对角线互相平分且相等可得点O到E、P、F、D的距离相等,从而判断出PD、EF为⊙O的直径,再根据直线与圆相切的定义可得PD⊥AC,然后根据正方形的性质求解即可.
解答:(1)证明:在正方形ABCD中,∠D=90°,
∵PE⊥DA,PF⊥CD,
∴∠PED=∠PFD=90°,
∴∠PED=∠PFD=∠EPF=∠D,
∴四边形EPFD为矩形;
(2)证明:如图,连接PD,
在正方形ABCD中,∠BAP=∠DAP,AB=AD,
在△ABP和△ADP中,
,
∴△ABP≌△ADP(SAS),
∴BP=DP,
由(1)知四边形EPFD是矩形,
∴EF=DP,
∴BP=EF;
(3)解:设DP、EF的交点为O,
∵四边形EPFD是矩形,
∴点O到E、P、F、D的距离相等,
∴点E、P、D、F四个点在同一个圆上,即⊙O上,对角线PD、EF为⊙O的直径,
∴当AC⊥PD时,AC为⊙O的切线,
此时,PA=PB=PC=PD=
AC=
×4
=2
,
故BP的长为2
.
∵PE⊥DA,PF⊥CD,
∴∠PED=∠PFD=90°,
∴∠PED=∠PFD=∠EPF=∠D,
∴四边形EPFD为矩形;
(2)证明:如图,连接PD,
在正方形ABCD中,∠BAP=∠DAP,AB=AD,

在△ABP和△ADP中,
|
∴△ABP≌△ADP(SAS),
∴BP=DP,
由(1)知四边形EPFD是矩形,
∴EF=DP,
∴BP=EF;
(3)解:设DP、EF的交点为O,
∵四边形EPFD是矩形,
∴点O到E、P、F、D的距离相等,
∴点E、P、D、F四个点在同一个圆上,即⊙O上,对角线PD、EF为⊙O的直径,
∴当AC⊥PD时,AC为⊙O的切线,
此时,PA=PB=PC=PD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故BP的长为2
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,矩形的判定与性质,切线的性质,熟记各图形的性质和判定方法是解题的关键.

练习册系列答案
相关题目
为迎接“五一”的到来,同学们做了许多拉花布置教室准备召开“五一”联欢晚会,小刚搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙距离应为( )
| A、0.7米 | B、0.8米 |
| C、0.9米 | D、1.0米 |

 用红、黄、绿三种不同的颜色给如图所示的两个小矩形随机涂色,每个矩形涂一种颜色.
用红、黄、绿三种不同的颜色给如图所示的两个小矩形随机涂色,每个矩形涂一种颜色. 海上有一座灯塔P,一客轮以60海里/时的速度由西向东航行,行至A处时测得灯塔P在北偏东60°方向,继续航行40分钟后,到B处又测得灯塔P在北偏东30°方向.
海上有一座灯塔P,一客轮以60海里/时的速度由西向东航行,行至A处时测得灯塔P在北偏东60°方向,继续航行40分钟后,到B处又测得灯塔P在北偏东30°方向. 如图,A是线段BF延长线上的点,矩形BCDF的外接圆O交AC的中点E.
如图,A是线段BF延长线上的点,矩形BCDF的外接圆O交AC的中点E. 如图,AB为⊙O的直径,CB⊥AB,连接OC过A作AD∥OC交⊙O于D,连接CD并延长交BA的延长线于E.
如图,AB为⊙O的直径,CB⊥AB,连接OC过A作AD∥OC交⊙O于D,连接CD并延长交BA的延长线于E. 如图,点O为∠APB角平分线上一点,半径为2的⊙O切PA于A点,AP=4.
如图,点O为∠APB角平分线上一点,半径为2的⊙O切PA于A点,AP=4.