题目内容
 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为67°,在教学楼三楼D处测得旗杆顶部的仰角为37°,旗杆底部与教学楼一楼在同一水平线上,已知每层的高度为3m,求旗杆AB的高度(精确到0.1m).(参考数据:tan67°≈
某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为67°,在教学楼三楼D处测得旗杆顶部的仰角为37°,旗杆底部与教学楼一楼在同一水平线上,已知每层的高度为3m,求旗杆AB的高度(精确到0.1m).(参考数据:tan67°≈| 12 |
| 5 |
| 3 |
| 4 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过点D作DE⊥AB,垂足为E,则四边形ACDE为矩形,AE=CD=6米,AC=DE.设BE=x米,先解Rt△BDE,得出DE=
x米,AC=
x米,再解Rt△ABC,得出AB=
x米,然后根据AB-BE=AE,列出关于x的方程,解方程即可.
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 5 |
解答: 解:过点D作DE⊥AB,垂足为E,由题意可知,四边形ACDE为矩形,
解:过点D作DE⊥AB,垂足为E,由题意可知,四边形ACDE为矩形,
则AE=CD=6米,AC=DE.
设BE=x米.
在Rt△BDE中,∵∠BED=90°,∠BDE=37°,
∴DE=
BE=
x米,
∴AC=DE=
x米.
在Rt△ABC中,∵∠BAC=90°,∠ACB=67°,
∴AB=
AC=
×
x=
x米,
∵AB-BE=AE,
∴
x-x=6,
∴x=
,
AB=
×
=
≈8.7(米).
即旗杆AB的高度约为8.7米.
 解:过点D作DE⊥AB,垂足为E,由题意可知,四边形ACDE为矩形,
解:过点D作DE⊥AB,垂足为E,由题意可知,四边形ACDE为矩形,则AE=CD=6米,AC=DE.
设BE=x米.
在Rt△BDE中,∵∠BED=90°,∠BDE=37°,
∴DE=
| 4 |
| 3 |
| 4 |
| 3 |
∴AC=DE=
| 4 |
| 3 |
在Rt△ABC中,∵∠BAC=90°,∠ACB=67°,
∴AB=
| 12 |
| 5 |
| 12 |
| 5 |
| 4 |
| 3 |
| 16 |
| 5 |
∵AB-BE=AE,
∴
| 16 |
| 5 |
∴x=
| 30 |
| 11 |
AB=
| 16 |
| 5 |
| 30 |
| 11 |
| 96 |
| 11 |
即旗杆AB的高度约为8.7米.
点评:此题考查了解直角三角形的应用-仰角俯角问题,作出辅助线,构造直角三角形是解题的关键.

练习册系列答案
相关题目
读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
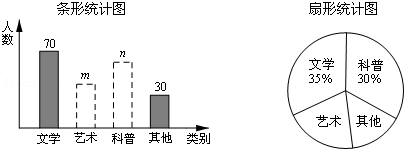
学校计划购买课外读物6000册,估计学校购买其他类读物大约有( )

学校计划购买课外读物6000册,估计学校购买其他类读物大约有( )
| A、300 | B、900 |
| C、30 | D、600 |
 如图是由八个相同小正方体组合而成的几何体,则其俯视图是( )
如图是由八个相同小正方体组合而成的几何体,则其俯视图是( )A、 |
B、 |
C、 |
D、 |
 如图,在平面直角坐标系中,矩形OABC的对角线AC=10,cos∠OCA=
如图,在平面直角坐标系中,矩形OABC的对角线AC=10,cos∠OCA= 海上有一座灯塔P,一客轮以60海里/时的速度由西向东航行,行至A处时测得灯塔P在北偏东60°方向,继续航行40分钟后,到B处又测得灯塔P在北偏东30°方向.
海上有一座灯塔P,一客轮以60海里/时的速度由西向东航行,行至A处时测得灯塔P在北偏东60°方向,继续航行40分钟后,到B处又测得灯塔P在北偏东30°方向. 如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度.
如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度. 如图,AB为⊙O的直径,CB⊥AB,连接OC过A作AD∥OC交⊙O于D,连接CD并延长交BA的延长线于E.
如图,AB为⊙O的直径,CB⊥AB,连接OC过A作AD∥OC交⊙O于D,连接CD并延长交BA的延长线于E. 如图,一张矩形纸片ABCD,其中AB=2,BC=3,将该纸片沿对角线BD折叠,则阴影部分的面积为
如图,一张矩形纸片ABCD,其中AB=2,BC=3,将该纸片沿对角线BD折叠,则阴影部分的面积为