题目内容
12.已知抛物线y=ax2+bx+c与双曲线y=$\frac{{k}^{2}}{x}$有三个交点A(-3,m),B(-1,n),C(2,p),则不等式ax3+bx2+cx-k2>0的解集为-3<x<-1或x>2.分析 根据题意,进行适当的变形,即可得到不等式ax3+bx2+cx-k2>0的解集,本题得以解决.
解答 解:∴抛物线y=ax2+bx+c与双曲线y=$\frac{{k}^{2}}{x}$有三个交点A(-3,m),B(-1,n),C(2,p),
∴xy1=ax3+bx2+cx,xy2=k2,
∴xy1-xy2=ax3+bx2+cx-k2,
∴不等式ax3+bx2+cx-k2>0的解集为:-3<x<-1或x>2,
故答案为:-3<x<-1或x>2.
点评 本题考查二次函数与不等式组,解题的关键是明确题意,利用数形结合的思想解答问题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
20. 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )| A. | (3,4)或(2,4) | B. | (2,4)或(8,4) | C. | (3,4)或(8,4) | D. | (3,4)或(2,4)或(8,4) |
17.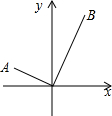 如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
 如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )| A. | 2$\sqrt{5}$ | B. | 4 | C. | $\sqrt{5}$ | D. | 2 |
 如图,在△ABC中,∠C=90°,∠A=30°,BC=5,在△DEF中,∠EDF=90°,∠DEF=45°,DE=3.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动,在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动到点F与点B重合为止),连接BE,设AD=x,BE=y.下列结论:①当x=2时,y=$\sqrt{73}$;②当x=10-4$\sqrt{3}$时,BE∥AC;③当x=7-3$\sqrt{2}$时,∠EBD=22.5°,其中正确有( )
如图,在△ABC中,∠C=90°,∠A=30°,BC=5,在△DEF中,∠EDF=90°,∠DEF=45°,DE=3.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动,在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动到点F与点B重合为止),连接BE,设AD=x,BE=y.下列结论:①当x=2时,y=$\sqrt{73}$;②当x=10-4$\sqrt{3}$时,BE∥AC;③当x=7-3$\sqrt{2}$时,∠EBD=22.5°,其中正确有( ) 如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连结ED,EC.
如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连结ED,EC. 如图,在矩形ABCD中,有以下结论:
如图,在矩形ABCD中,有以下结论: 如图,已知菱形ABCD中,AC,BD相交于点O,点E是AB的中点,OE=5cm,则菱形的周长是40cm.
如图,已知菱形ABCD中,AC,BD相交于点O,点E是AB的中点,OE=5cm,则菱形的周长是40cm.