题目内容
18.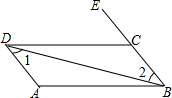 如图:由∠1=∠2,可以得出AD∥BC,理由是内错角相等,两直线平行;
如图:由∠1=∠2,可以得出AD∥BC,理由是内错角相等,两直线平行;由AB∥CD,可以得出∠ABC=∠ECD,理由是两直线平行,同位角相等;
由∠ADC+∠DCB=180°,可以得出AD∥BC,理由是同旁内角互补,两直线平行.
分析 根据平行线的判定和性质定理即可得到结论.
解答 如图:由∠1=∠2,可以得出AD∥BC,理由是 内错角相等,两直线平行;
由AB∥CD,可以得出∠ABC=∠ECD,理由是两直线平行,同位角相等;
由∠ADC+∠DCB=180°,可以得出AD∥BC,理由是同旁内角互补,两直线平行.
故答案为:AD∥BC,内错角相等,两直线平行,两直线平行,同位角相等,同旁内角互补,两直线平行.
点评 本题考查了平行线的判定和性质,熟练掌握平行线的判定和性质是解题的关键.

练习册系列答案
相关题目
3.在函数y=$\frac{-2}{x}$的图象上的点是( )
| A. | (1,2) | B. | (0,2) | C. | (1,-2) | D. | (1,0) |
8.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,根据四人各自的平均成绩,公司将录取乙.
| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩(百分制) | 面试 | 86 | 92 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
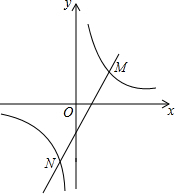 如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象交于点M(2,m)、N(-1,-4)两点,则kx+b>$\frac{a}{x}$的解集为x<-1或x>2.
如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象交于点M(2,m)、N(-1,-4)两点,则kx+b>$\frac{a}{x}$的解集为x<-1或x>2.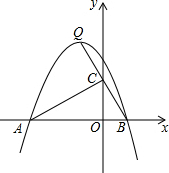 如图,抛物线y=ax2-2x+c经过点P(-2,3),顶点Q的横坐标为-1,设抛物线与x轴相交于点A,B.
如图,抛物线y=ax2-2x+c经过点P(-2,3),顶点Q的横坐标为-1,设抛物线与x轴相交于点A,B.