题目内容
14.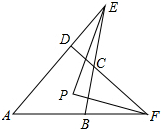 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°.(1)求证:∠CBF=∠ADC;
(2)求∠PEB+∠PFC;
(3)求∠EPF.
分析 (1)根据四边形的内角和,可得∠ADC+∠ABC,根据邻补角的定义,可得∠ABC+∠CBF,根据等量代换,可得答案;
(2)根据三角形的内角和定理,可得∠A+∠ADC+∠AFD,∠A+∠AEB+∠ABE,根据等式的性质,可得∠AFD+∠AEB,根据角平分线的性质,可得答案;
(3)根据等式的性质,可得∠EPF+∠PFD=∠AEP+∠EDF,根据三角形外角的性质,可得∠EDF=∠A+∠AFD,根据等式的性质,可得答案.
解答 (1)证明:∵∠A=44°,∠BCD=136°,
∴∠ADC+∠ABC=360°-∠A-∠BCD=180°.
∵∠ABC+∠CBF=180°,
∴∠CBF=∠ADC;
(2)解:∵∠A+∠ADC+∠AFD=180°,∠A+∠AEB+∠ABE=180°,
∴2∠A+∠ADC+∠ABE+∠AFD+∠AEB=360°,
∴∠AFD+∠AEB=360°-2×44°-180°=92°,
∵∠AEB、∠AFD的平分线交于点P,
∴∠PEB+∠PFC=$\frac{1}{2}$(∠AEB+∠AFD)=$\frac{1}{2}$×92°=46°;
(3)∵∠EPF+∠PFD=∠AEP+∠EDF,
而∠EDF=∠A+∠AFD=∠A+2∠PFD,
∴∠EPF+∠PFD=∠AEP+∠A+2∠PFD,
∴∠EPF=∠A+∠AEP+∠PFD=44°+46°=90°.
点评 本题考查了三角形内角和定理,利用了三角形的内角和,三角形外角的性质,利用等式的性质得出∠EPF+∠PFD=∠AEP+∠EDF是解题关键.
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
19.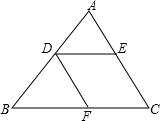 如图,DF∥AC,DE∥BC,下列各式中正确的是( )
如图,DF∥AC,DE∥BC,下列各式中正确的是( )
 如图,DF∥AC,DE∥BC,下列各式中正确的是( )
如图,DF∥AC,DE∥BC,下列各式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{BF}{CF}$ | B. | $\frac{AE}{DE}$=$\frac{CE}{BC}$ | C. | $\frac{AE}{CE}$=$\frac{BD}{CD}$ | D. | $\frac{AD}{DE}$=$\frac{AB}{BC}$ |
 如图,已知EF是矩形ABCD内一条线段,EF∥BC,直线BE、CF交于点P,直线AE、DF交于点Q,求证:PQ⊥EF.
如图,已知EF是矩形ABCD内一条线段,EF∥BC,直线BE、CF交于点P,直线AE、DF交于点Q,求证:PQ⊥EF.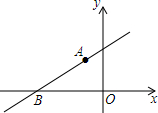 如图,直线y=kx+b经过A(-1,1)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-x的解集为-$\sqrt{7}$<x<-1.
如图,直线y=kx+b经过A(-1,1)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-x的解集为-$\sqrt{7}$<x<-1. 如图,在△ABC中,AB>AC,AD为∠BAC的平分线,AD的垂直平分线交BC的延长线于点F,交AB、AC于点E、G.
如图,在△ABC中,AB>AC,AD为∠BAC的平分线,AD的垂直平分线交BC的延长线于点F,交AB、AC于点E、G.
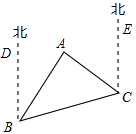 如图,A点在B点的北偏东40°方向,C点在B点的北偏东75°方向,A点在C点的北偏西50°方向,求从A点观测B,C两点的视角∠BAC的度数.
如图,A点在B点的北偏东40°方向,C点在B点的北偏东75°方向,A点在C点的北偏西50°方向,求从A点观测B,C两点的视角∠BAC的度数.