题目内容
19.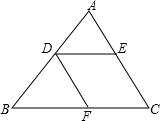 如图,DF∥AC,DE∥BC,下列各式中正确的是( )
如图,DF∥AC,DE∥BC,下列各式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{BF}{CF}$ | B. | $\frac{AE}{DE}$=$\frac{CE}{BC}$ | C. | $\frac{AE}{CE}$=$\frac{BD}{CD}$ | D. | $\frac{AD}{DE}$=$\frac{AB}{BC}$ |
分析 根据平行线分线段成比例,由DF∥AC得到$\frac{AD}{BD}$=$\frac{CF}{BF}$,则可对A进行判断;由DE∥BC得到$\frac{AE}{EC}$=$\frac{AD}{BD}$,则可对C进行判断;利用等量代换接着得到$\frac{AE}{CE}$=$\frac{DE}{BF}$,则可对B进行判断;然后由DE∥BC得到$\frac{AD}{AB}$=$\frac{DE}{BC}$,则可对D进行判断.
解答 解:∵DF∥AC,
∴$\frac{AD}{BD}$=$\frac{CF}{BF}$,所以A选项错误;
∵DE∥BC,
∴$\frac{AE}{EC}$=$\frac{AD}{BD}$,所以C选项错误;
而$\frac{AD}{BD}$=$\frac{CF}{BF}$,
∴$\frac{AE}{CE}$=$\frac{CF}{BF}$,
∵DE∥CF,DF∥CE,
∴四边形DECF为平行四边形,
∴CF=DE,
∴$\frac{AE}{CE}$=$\frac{DE}{BF}$,即$\frac{AE}{DE}$=$\frac{CE}{BF}$,所以B选项错误;
∵DE∥BC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,即$\frac{AD}{DE}$=$\frac{AB}{BC}$,所以D选项正确.
故选D.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了比例的性质.

练习册系列答案
相关题目
2.10袋小麦称重记录如下,以每袋40kg为准,超出千克数记为正数,不足千克数记为负数,10袋小麦超过多少kg?10袋小麦的重量是多少?
| +7 | +5 | -4 | +6 | +4 | +3 | -3 | -2 | +8 | +1 |
7.已知△ABC∽△A′B′C′,AD、A′D′分别是△ABC和△A′B′C′的对应高,且AD:A′D′=2:3,则下列结论正确的是( )
| A. | AB:A′B′=2:3 | B. | S△ABC:S△A′B′C′=2:3 | ||
| C. | (AB+BC+AC):(A′B′+B′C′+A′C′)=4:9 | D. | (AD+BC):(A′D′+B′C′)=4:9 |
8. 如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )
如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )
 如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )
如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{5}{4}$ |
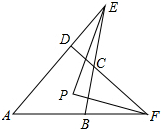 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°. 在如图所示的方格中分别填入-8,-6,-4,-2,2,4,6,8这8个数,使得每行的三个数,每列的三个数,斜对角的三个数之和都相等.
在如图所示的方格中分别填入-8,-6,-4,-2,2,4,6,8这8个数,使得每行的三个数,每列的三个数,斜对角的三个数之和都相等.