题目内容
5. 如图,已知EF是矩形ABCD内一条线段,EF∥BC,直线BE、CF交于点P,直线AE、DF交于点Q,求证:PQ⊥EF.
如图,已知EF是矩形ABCD内一条线段,EF∥BC,直线BE、CF交于点P,直线AE、DF交于点Q,求证:PQ⊥EF.
分析 由四边形ABCD是矩形,得到AD∥BC,AD=BC,于是得到AD∥BC∥EF,推出△AQD∽△EQF,△BPC∽△EPF,根据相似三角形的性质得到$\frac{AQ}{EQ}=\frac{AD}{EF}$,$\frac{BP}{EP}=\frac{BC}{EF}$,根据比例的性质得到$\frac{AE}{EQ}=\frac{BE}{EP}$,证得△AEB∽△QEP,得到对应角相等∠ABE=∠EPQ,于是证得AB∥PQ,即可得到结论.
解答  证明:∵四边形ABCD是矩形,
证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵EF∥BC,
∴AD∥BC∥EF,
∴△AQD∽△EQF,△BPC∽△EPF,
∴$\frac{AQ}{EQ}=\frac{AD}{EF}$,$\frac{BP}{EP}=\frac{BC}{EF}$,
∴$\frac{AQ}{EQ}=\frac{BP}{EP}$,
∴$\frac{AQ}{BP}=\frac{EQ}{EP}$,
∵AQ=EQ+AE,BP=EP+BE,
∴$\frac{AQ}{BP}=\frac{EQ}{EP}=\frac{AE}{BE}$,
∴$\frac{AE}{EQ}=\frac{BE}{EP}$,
∵∠AEB=∠QEP,
∴△AEB∽△QEP,
∴∠ABE=∠EPQ,
∴AB∥PQ,
∵EF∥AD,
∴PQ⊥EF.
点评 本题考查了相似三角形的判定和性质,矩形的性质,平行线的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
9.若某二次函数的x与y的部分对应值如表:
(1)根据表格,试说明该函数图象的对称轴、顶点坐标和开口方向;
(2)当x为何值时,y随x的增大而增大;
(3)求出该函数的解析式.
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
(2)当x为何值时,y随x的增大而增大;
(3)求出该函数的解析式.
17.下列长度的3条线段,能首尾依次相接组成三角形的是( )
| A. | 1cm,2cm,3cm | B. | 8cm,6cm,4cm | C. | 12cm,5cm,6cm | D. | 1cm,2cm,4cm |
 按图那样堆放钢管,第一层(最上层)有5根,第二层有6根,第三层有7根,…那么,第n层有多少根?并求出第30层钢管的根数.
按图那样堆放钢管,第一层(最上层)有5根,第二层有6根,第三层有7根,…那么,第n层有多少根?并求出第30层钢管的根数.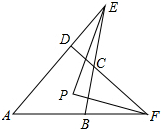 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°.