题目内容
3.如图,在Rt△ABC中,AC=BC,P为射线BC上一动点,PD⊥AB于D,F是PC中点,EF∥AC,交直线AB于点E,探究线段ED、AB的数量关系,并证明你的结论.
分析 过C作CN⊥AB于N,PD和EF交于M,连接CM,求出四边形MDNC是矩形,推出NC=DM,求出NC=$\frac{1}{2}$AB,根据等腰直角三角形性质求出DE=DM,即可得出答案.
解答 解:ED=$\frac{1}{2}$AB,
理由是: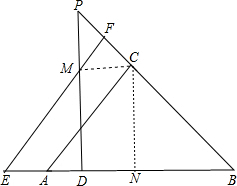
过C作CN⊥AB于N,PD和EF交于M,连接CM,
∵AC=CB,∠ACB=90°,
∴∠CAB=∠B=45°,
∵AC∥EF,
∴∠FEB=∠CAB=45°,∠EFB=∠ACB=90°,
∵PD⊥AB,PF=FC,
∴∠MDE=∠PDB=90°,MP=CM,
∴∠EMD=45°,∠DPB=45°,
∴DE=DM,∠MPC=∠MCP=45°,
∴∠PMC=∠DMC=90°,
∵∠FND=90°,
∴四边形MDNC是矩形,
∴CN=AN=BN,
∵∠ACB=90°,CN⊥AB,
∴AN=BN,
∴CN=$\frac{1}{2}$AB,
∴ED=$\frac{1}{2}$AB.
点评 本题考查了直角三角形的性质,等腰直角三角形的性质和判定,矩形的性质和判定,三角形的内角和定理的应用,能正确作出辅助线是解此题的关键.

练习册系列答案
相关题目
8. 如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )
如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )
 如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )
如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{5}{4}$ |
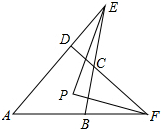 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°.
 如图,Rt△ABC中,∠ACB=90°,DE⊥AB交AC于F,则图中有6对相似三角形.
如图,Rt△ABC中,∠ACB=90°,DE⊥AB交AC于F,则图中有6对相似三角形.