题目内容
10．一棵挺直的松树高18米，一阵强风将其折断，树尖B落在离树的底端O点12米处，求该树断处的高度OA．分析 根据题意构造直角三角形，然后设OA=x米，然后表示出AB的长度，从而利用勾股定理列出方程求解即可．
解答 
解：如图，∵根据题意得：OA+AB=18，OB=12，
∴设OA=x米，则AB=（18-x）米，
∴x2+122=（18-x）2，
解得：x=5，
∴该树断处的高度为OA．
点评 本题考查了勾股定理的应用，解题的关键是从实际问题中构造出直角三角形，难度不大．
练习册系列答案
相关题目
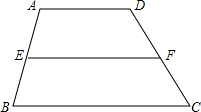如图，在四边形ABCD中，AD∥BC，E、F分别是AB、CD两边的中点，求证：EF∥AD∥BC，EF=$\frac{1}{2}$（AD+BC）
18．已知n是一个正整数，若$\sqrt{135n}$与$\sqrt{3}$能合并，则n的最小值是（ ）
| A． | 3 | B． | 5 | C． | 15 | D． | 25 |
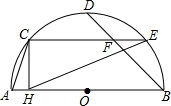如图，AB是半圆O的直径，C、D、E是半圆的四等分点，CH⊥AB于H，连接BD、