Question

5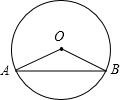．（1）如图，弦AB把⊙O分成2：7，∠AOB=80°；
（2）在⊙O中，弦AB的长恰好等于半径，$\widehat{AB}$的度数为60°．

Answer 1

分析 （1）根据圆心角、弧、弦的关系，点A、B把⊙O分成2：7两条弧，则把360度的圆心角为分为2：7部分，然后计算360°的$\frac{2}{9}$份即可得到∠AOB的度数．
（2）由弦AB的长等于⊙O的半径，可得△AOB为等边三角形，且∠AOB=60°，则易求$\widehat{AB}$的度数．

解答 解：（1）∠AOB的度数=$\frac{2}{9}$×360°=80°．
故答案为：80．

（2）∵弦AB的长等于⊙O的半径，
∴△AOB为等边三角形，
∴∠AOB=60°，
∴$\widehat{AB}$的度数是：60°．
故答案是：60°．

点评 本题考查了圆心角、弧、弦的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．