题目内容
20.观察、发现:$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\frac{\sqrt{2}-1}{(\sqrt{2})^{2}-1}$=$\frac{\sqrt{2}-1}{2-1}$=$\sqrt{2}$-1(1)试化简:$\frac{1}{\sqrt{3}+\sqrt{2}}$;
(2)直接写出:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;
(3)求值:$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$.
分析 根据题目给出的过程即可求出答案.
解答 解:(1)原式=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}-\sqrt{2}}{3-2}=\sqrt{3}-\sqrt{2}$;
(2)原式=$\frac{(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}-\sqrt{n}$;
故答案为:$\sqrt{n+1}-\sqrt{n}$
(3)由(2)可知:
原式=$\sqrt{2}$-1+$\sqrt{3}-\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{100}$-$\sqrt{99}$
=-1+$\sqrt{100}$
=9
点评 本题考查二次根式的混合运算,涉及平方差公式,属于基础题型.

练习册系列答案
相关题目
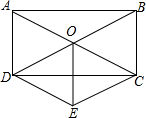 如图,矩形ABCD的两条对角线交于点O,DE∥AC,CE∥DB,DE和CE交于点E,求证:OE和CD互相垂直平分.
如图,矩形ABCD的两条对角线交于点O,DE∥AC,CE∥DB,DE和CE交于点E,求证:OE和CD互相垂直平分.

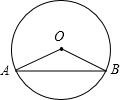 (1)如图,弦AB把⊙O分成2:7,∠AOB=80°;
(1)如图,弦AB把⊙O分成2:7,∠AOB=80°;