题目内容
9.某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定,现从两家提供的样品中各抽取了6件进行检查,超过标准质量部分记为正数,不足部分记为负数,若该皮具的标准质量为500克,测得它们质量如下(单位:g)| 厂家 | 超过标准质量的部分 | |||||
| 甲 | -3 | 0 | 0 | 1 | 2 | 0 |
| 乙 | -2 | 1 | -1 | 0 | 1 | 1 |
(2)通过计算,你认为哪一家生产皮具的质量比较稳定?
分析 (1)求出记录的质量的和,再加上标准质量,计算即可得解;
(2)以标准质量为基准,根据方差的定义计算两公司的方差,方差小的质量比较稳定.
解答 解:(1)甲厂抽样检测的皮具总质量为500×6+(-3+0+0+1+2+0)=3000(克),
乙厂抽样检测的皮具总质量为500×6+(-2+1-1+0+1+1)=3000(克);
(2)∵$\overline{{x}_{甲}}$=$\frac{1}{6}$×(-3+0+0+1+2+0)=0,
∴${{S}_{甲}}^{2}$=$\frac{1}{6}$×[(-3-0)2+(0-0)2×3+(1-0)2+(2-0)2]≈2.33,
∵$\overline{{x}_{乙}}$=$\frac{1}{6}$×(-2+1-1+0+1+1)=0,
∴${{S}_{乙}}^{2}$=$\frac{1}{6}$×[(-2-0)2+3×(1-0)2+(-1-0)2+(0-0)2]≈1.33,
∵${{S}_{乙}}^{2}$<${{S}_{甲}}^{2}$,
∴乙公司生产皮具的质量比较稳定.
点评 本题主要考查方差,用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果叫方差.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.在对-$\frac{3}{4}$a2x+3axy2进行因式分解时,公因式最好是( )
| A. | ax | B. | $\frac{3}{4}$ax | C. | -$\frac{3}{4}$ax | D. | -$\frac{1}{4}$ax |
1.下列各数表示正确的是( )
| A. | 5700000=57×106 | |
| B. | 0.0158(用四舍五入法精确到0.001)≈0.015 | |
| C. | 0.0000275=2.75×10-6 | |
| D. | 1.967(用四舍五入法精确到十分位)≈2.0 |
18.(1)问题背景
如图甲,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.

请直接写出四边形ABCD的面积为25.
(2)类比迁移
如图乙,P为等边△ABC外一点,BP=1,CP=3,且∠BPC=120°,求四边形ABPC的面积.
(3)拓展延伸
如图丙,在五边形ABCDE中,BC=4,CD+AB=4,AE=DE=6,AE⊥AB,DE⊥CD,求五边形ABCDE的面积.
如图甲,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.

小明发现四边形ABCD的一组领边AD=CD,这就为旋转作了铺垫.于是,小明同学有如下思考过程: 第一步:将△ADE绕点D逆时针旋转90°; 第二步:利用∠A与∠DCB互补, 证明F、C、B三点共线, 从而得到正方形DEBF; 进而求得四边形ABCD的面积. 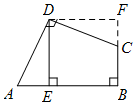 |
(2)类比迁移
如图乙,P为等边△ABC外一点,BP=1,CP=3,且∠BPC=120°,求四边形ABPC的面积.
(3)拓展延伸
如图丙,在五边形ABCDE中,BC=4,CD+AB=4,AE=DE=6,AE⊥AB,DE⊥CD,求五边形ABCDE的面积.
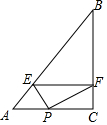 如图,△ABC中,∠C=90°,BC=4,AC=3,P是边AC上的一动点,PE⊥AB于点E,EF⊥BC于点F.设AP=x,则能使以点P、C、F为顶点的三角形与以A、P、E为顶点的三角形相似的x=$\frac{75}{34}$或$\frac{75}{41}$.
如图,△ABC中,∠C=90°,BC=4,AC=3,P是边AC上的一动点,PE⊥AB于点E,EF⊥BC于点F.设AP=x,则能使以点P、C、F为顶点的三角形与以A、P、E为顶点的三角形相似的x=$\frac{75}{34}$或$\frac{75}{41}$.