题目内容
4.(1 )将点A(4,0)绕着原点O按顺时针方向旋转30°,则其对应点A′的坐标是(2$\sqrt{3}$,-2);(2)将点A(4,0)绕着原点O按逆时针方向旋转60°,则其对应点A″的坐标是(2,2$\sqrt{3}$);
(3)在平面直角坐标系中,以原点O为中心,把点A(4,5)逆时针旋转90°,得到的点坐标为(-5,4).
分析 (1)根据旋转中心为原点,旋转方向顺时针,旋转角度30°,作出点A的对称图形A′,作A′B⊥x轴于点B,利用30°的函数值求得OB,A′B的长,进而根据A′所在象限可得所求点的坐标.
(2)连接OA″,过点A″作A″B′⊥x轴于点B′,根据点A的坐标以及旋转变换的性质可得OA″的长度,∠A″OB′=60°,然后解直角三角形求出OB′、A″B′的长度,从而得解.
(3)首先根据点A的坐标求出OA的长度,然后根据旋转变换只改变图形的位置,不改变图形的形状与大小,可得OA′=OA,据此求出点A′的坐标即可.
解答  解:(1)如图1,作A′B⊥x轴于点B,
解:(1)如图1,作A′B⊥x轴于点B,
∵OA′=OA=4,∠AOA′=30°,
∴A′B=$\frac{1}{2}$OA′=2,OB=OA×cos30°=2$\sqrt{3}$.
故答案为:A′(2$\sqrt{3}$,-2).
(2)如图1,连接OA″,过点A″作A″B′⊥x轴于点B′,
∵点A(4,0),
∴OA=4,
∵点A(4,0)绕着原点O逆时针方向旋转60°角到对应点A″,
∴OA″=OA=4,∠A″OB′=60°,
∴OB′=OA″cos60°=4×$\frac{1}{2}$=2,
A″B′=OA″sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
所以,点A″的坐标是(2,2$\sqrt{3}$).
故答案为(2,2$\sqrt{3}$).
(3) 如图2,过点A作AC⊥y轴于点C,作AB⊥x轴于点B,过A′作A′E⊥y轴于点E,作A′D⊥x轴于点D,
如图2,过点A作AC⊥y轴于点C,作AB⊥x轴于点B,过A′作A′E⊥y轴于点E,作A′D⊥x轴于点D,
∵点A(4,5),
∴AC=4,AB=5,
∵点A(4,5)绕原点逆时针旋转90°得到点A′,
∴A′E=AB=5,A′D=AC=4,
∴点A′的坐标是(-5,4).
故答案为:(-5,4).
点评 此题主要考查了坐标与图形变换-旋转,要熟练掌握,解答此题的关键是要明确:旋转变换只改变图形的位置,不改变图形的形状与大小.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| 厂家 | 超过标准质量的部分 | |||||
| 甲 | -3 | 0 | 0 | 1 | 2 | 0 |
| 乙 | -2 | 1 | -1 | 0 | 1 | 1 |
(2)通过计算,你认为哪一家生产皮具的质量比较稳定?
| A. | ∵(2x-2)(3x-4)=0,∴2x-2=0或3x-4=0 | B. | ∵(x+3)(x-1)=1,∴x+3=0或x-1=1 | ||
| C. | ∵(x-2)(x-3)=2×3,∴x-2=2或x-3=3 | D. | ∵x(x+2)=0,∴x+2=0 |
 如图:⊙O的直径AB⊥CD于P,AP=CD=4cm,则OP=$\frac{5}{2}$cm.
如图:⊙O的直径AB⊥CD于P,AP=CD=4cm,则OP=$\frac{5}{2}$cm.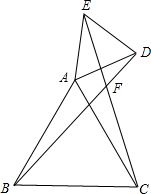 已知:如图所示,△ABC与△ADE均为等边三角形,点A为它们公共顶点,现连接BD、EC,BD与EC交于F点:
已知:如图所示,△ABC与△ADE均为等边三角形,点A为它们公共顶点,现连接BD、EC,BD与EC交于F点: