题目内容
19.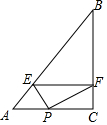 如图,△ABC中,∠C=90°,BC=4,AC=3,P是边AC上的一动点,PE⊥AB于点E,EF⊥BC于点F.设AP=x,则能使以点P、C、F为顶点的三角形与以A、P、E为顶点的三角形相似的x=$\frac{75}{34}$或$\frac{75}{41}$.
如图,△ABC中,∠C=90°,BC=4,AC=3,P是边AC上的一动点,PE⊥AB于点E,EF⊥BC于点F.设AP=x,则能使以点P、C、F为顶点的三角形与以A、P、E为顶点的三角形相似的x=$\frac{75}{34}$或$\frac{75}{41}$.
分析 利用勾股定理列式求出AB,再设AP=a,利用∠A的余弦表示出AE,再求出BE,利用∠B的余弦求出BF,然后求出CF,再根据相似三角形对应边成比例求出$\frac{CF}{PF}$,然后求解即可.
解答 解:在∠C=90°,BC=4,AC=3,
由勾股定理得,AB=5,
设AP=x,
则AE=AP•cosA=$\frac{3}{5}$x,
所以,BE=5-$\frac{3}{5}$x,
BF=BE•cosB=$\frac{4}{5}$×(5-$\frac{3}{5}$x)=4-$\frac{12}{25}$x,
所以,CF=4-(4-$\frac{12}{25}$x)=$\frac{12}{25}$x,
∵△PCF与△APE相似,
∴$\frac{PC}{CF}$=$\frac{AE}{PE}$,或$\frac{PC}{CF}$=$\frac{PE}{AE}$,
即$\frac{3-x}{\frac{12}{25}x}$=$\frac{3}{4}$或$\frac{3-x}{\frac{12}{25}x}$=$\frac{4}{3}$,
解得x=$\frac{75}{34}$或x=$\frac{75}{41}$,
故答案为:$\frac{75}{34}$或$\frac{75}{41}$.
点评 本题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解题的关键,难点在于(2)利用锐角三角函数表示出相应的边并分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定,现从两家提供的样品中各抽取了6件进行检查,超过标准质量部分记为正数,不足部分记为负数,若该皮具的标准质量为500克,测得它们质量如下(单位:g)
(1)分别计算甲、乙两厂抽样检测的皮具总质量各是多少克?
(2)通过计算,你认为哪一家生产皮具的质量比较稳定?
| 厂家 | 超过标准质量的部分 | |||||
| 甲 | -3 | 0 | 0 | 1 | 2 | 0 |
| 乙 | -2 | 1 | -1 | 0 | 1 | 1 |
(2)通过计算,你认为哪一家生产皮具的质量比较稳定?
 如图,等腰Rt△ABC的顶点B落在直线l2上,若∠1=75°,∠2=60°.求证:l1∥l2.
如图,等腰Rt△ABC的顶点B落在直线l2上,若∠1=75°,∠2=60°.求证:l1∥l2.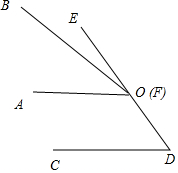 两个角∠BOA和∠EDC,∠AOB保持不动,∠EDC的一边CD∥AO,另一边DE与直线OB相交于点F.
两个角∠BOA和∠EDC,∠AOB保持不动,∠EDC的一边CD∥AO,另一边DE与直线OB相交于点F.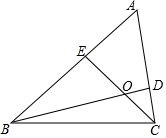 如图,D、E分别为△ABC的AC、AB边上的点,BD、CE相交于点O,若S△DOC=2,S△BOE=3,S△BOC=6,则S四边形AEOD=3.4.
如图,D、E分别为△ABC的AC、AB边上的点,BD、CE相交于点O,若S△DOC=2,S△BOE=3,S△BOC=6,则S四边形AEOD=3.4.