题目内容
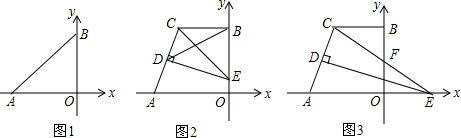
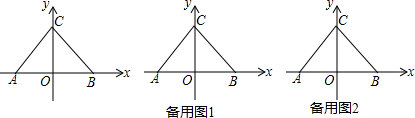
9.如图,在平面直角坐标系中,AC⊥BC于点C,且点C在y的正半轴上,点A和点B分别在x的负半轴和正半轴,AC=BC,AB=8.(1)求点C的坐标;
(2)点D从点C出发以1个单位/秒的速度向y的负半轴方向运动,同时点G从点B出发以1个单位/秒的速度向x轴的正方向运动,连接DG交直线BC于点F.设D、G两点运动时间为t秒,△DOF的面积为s,请用t的式子表示s,并直接写出t的取值范围;
(3)在(2)的条件下,过点F作FP⊥DF,过点C作x轴的平行线交FP于点P,连接AD,是否存在t,使△CPF的面积等于△AOD面积的2倍?如果存在,请求出t的值;如果不存在,请说明理由.
分析 (1)由直角三角形的性质和AC=BC,AB=8计算即可;
(2)由运动表示出OD=4-t,OG=4+t,利用面积公式计算即可;
(3)先判断△POI为等腰直角三角形,利用面积公式表示出△CPF和△AOD的面积,用2倍建立方程,解出即可.
解答 解:(1)∵AC=BC,AB=8,
∴OB=4,
∵AC⊥BC,AC=BC,
∴∠OBC=45°.
∵∠BOC=90°,
∴OC=OB=4,
∵点C在y的正半轴上,
∴C(0,4);
(2)过点D作DH∥x轴交直线BC于点H,可证CD=DH=BG
当0<t<4时,如图1,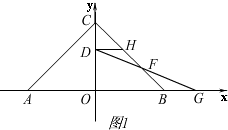
∵OD=4-t,OG=4+t,
∴S=$\frac{1}{2}$OD×OG=$\frac{1}{2}$(4-t)(4+t)=8-$\frac{1}{2}$t2,
如图2,当t>4时,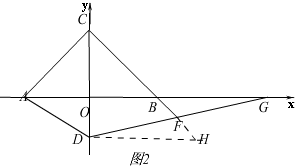
∵OD=t-4,OG=4+t,
∴S=$\frac{1}{2}$OD×OG=$\frac{1}{2}$(t-4)(4+t)=$\frac{1}{2}$t2-8,
(3)如图3,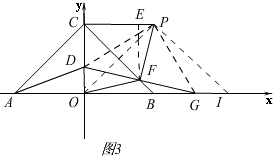
连接PD、PG、PO,过点F作E⊥CP于点E,过点P作PI⊥PO交x轴于点I,
∴△POI为等腰直角三角形,且OB=BI=OC=CP,
∴点P(4,4),CP=4.
当0≤t<4时,EF=$\frac{1}{2}$t+2,
S△CPF=$\frac{1}{2}$CP×EF=$\frac{1}{2}$×4×($\frac{1}{2}$t+2)=t+4
S△AOD=$\frac{1}{2}$OA×OD=$\frac{1}{2}$×4×(4-t)=8-2t
∴t+4=2(8-2t),
解得t=$\frac{12}{5}$,
当t>4时,EF=$\frac{1}{2}$t+2,
S△CPF=$\frac{1}{2}$CP×EF=$\frac{1}{2}$×4×($\frac{1}{2}$t+2)=t+4
S△AOD=$\frac{1}{2}$OA×OD=$\frac{1}{2}$×4×(t-4)=2t-8
∴t+4=2(2t-8),
解得t=$\frac{20}{3}$.
∴存在t,使△CPF的面积等于△AOD面积的2倍,t=$\frac{12}{5}$或t=$\frac{20}{3}$.
点评 此题是三角形综合题,主要考查了直角三角形的性质,面积计算方法,解本题的关键是面积的计算方法.作出辅助线是解本题的难点.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案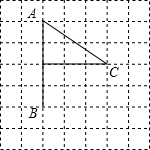 如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )| A. | (2,3) | B. | (1,3) | C. | (3,1) | D. | (3,0) |
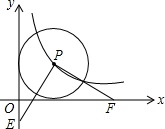 如图,点P为反比例函数y=$\frac{1}{x}$(x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是OF-OE=2或OE-OF=2或OF+OE=2.
如图,点P为反比例函数y=$\frac{1}{x}$(x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是OF-OE=2或OE-OF=2或OF+OE=2. 如图,四边形ABCD是矩形,将矩形折叠,使得点D落在BC边上.折痕经过点A,作出折叠后的图形(要求尺规作图,保留作图痕迹,不写作法)
如图,四边形ABCD是矩形,将矩形折叠,使得点D落在BC边上.折痕经过点A,作出折叠后的图形(要求尺规作图,保留作图痕迹,不写作法)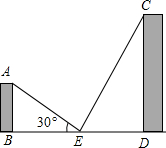 如图,两座建筑物AB与CD,其地面距离BD为60米,E为BD的中点,从E点测得A的仰角为30°,从C处测得E的俯角为60°,现准备在点A与点C之间拉一条绳子挂上小彩旗(不计绳子弯曲),求绳子AC的长度.(结果保留一位小数,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,两座建筑物AB与CD,其地面距离BD为60米,E为BD的中点,从E点测得A的仰角为30°,从C处测得E的俯角为60°,现准备在点A与点C之间拉一条绳子挂上小彩旗(不计绳子弯曲),求绳子AC的长度.(结果保留一位小数,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)