题目内容
11.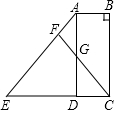 如图,矩形ABCD,E为射线CD上一点,连接AE,F为AE上一点,FC交AD于点G,FA=FG.求证:FE=FC.
如图,矩形ABCD,E为射线CD上一点,连接AE,F为AE上一点,FC交AD于点G,FA=FG.求证:FE=FC.
分析 由等腰三角形的性质得出∠2=∠1.由对顶角相等得出∠3=∠1,根据等量关系得出∠2=∠3,再根据矩形的性质和等量关系得出∠E=∠4,再由等腰三角形的性质即可得出结论.
解答 证明:如图, ∵FA=FG,
∵FA=FG,
∴∠2=∠1.
∵∠3=∠1,
∴∠2=∠3.
∵四边形ABCD是矩形,
∴∠ADC=90°.
∴∠E=90°-∠2,∠4=90°-∠3.
∴∠E=∠4.
∴FE=FC.
点评 本题考查了矩形的性质、等腰三角形的性质、直角三角形的性质、对顶角相等的性质;熟练掌握矩形的性质是解决问题的关键.

练习册系列答案
相关题目
2.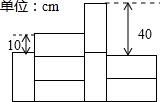 如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )
如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )
 如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )
如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )| A. | 425cm2 | B. | 525cm2 | C. | 600cm2 | D. | 800cm2 |
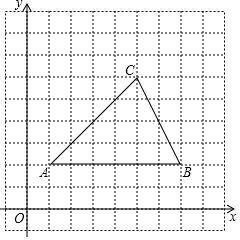 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(1,2),B(7,2),C(5,6).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(1,2),B(7,2),C(5,6).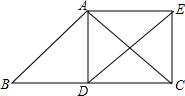 如图,在△ABC中,AB=AC,点D为边BC的中点,以AB、BD为邻边作?ABDE,连结AD、EC.
如图,在△ABC中,AB=AC,点D为边BC的中点,以AB、BD为邻边作?ABDE,连结AD、EC.