题目内容
3.请直接写出一个与$\sqrt{8}$是同类二次根式的最简二次根式$\sqrt{2}$.分析 根据最简二次根式与同类二次根式的定求解即可.
解答 解:$\sqrt{8}$=2$\sqrt{2}$与$\sqrt{2}$是同类二次根式,
故答案为:$\sqrt{2}$.
点评 此题主要考查了同类二次根式的定义,即:二次根式化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
13.邮递员从山坡下的邮局出发,骑自行车到达山坡顶后,停下一段时间分发邮件,之后沿原路返回邮局,设邮递员从邮局出发后所用的时间为x(分钟),邮递员与邮局的距离为y(米),则y与x的函数图象大致是( )
| A. | 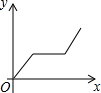 | B. | 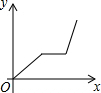 | C. | 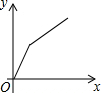 | D. | 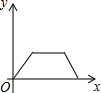 |
8.求一个正数的立方根,有些数可以直接求得,如$\root{3}{8}$=2,有些数则不能直接求得,如$\root{3}{9}$,但可以利用计算器求得,还可以通过一组数的内在联系,运用规律求得,请同学观察下表:
已知$\root{3}{2.16}$≈1.293,$\root{3}{21.6}$≈2.785,$\root{3}{216}$≈6,运用你发现的规律求$\root{3}{21600000}$=278.5.
| n | 0.008 | 8 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 0.2 | 2 | 20 | 200 | … |
15.已知$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b为常数,且ab≠0)表示焦点在x轴上的双曲线,若$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m-4}$=1表示焦点在x轴上的双曲线,则m的取值范围是( )
| A. | m>2 | B. | m>-3 | C. | m≥-3 | D. | -3<m<2 |
13. 如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )
如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )
 如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )
如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )| A. | ($\frac{1}{3}$,1) | B. | ($\frac{2}{3}$,1) | C. | (1,$\frac{2}{3}$) | D. | (1,2) |
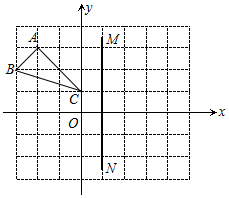 已知△ABC在平面直角坐标系中的位置如图所示,每个小正方形的边长为1,点ABC都在格点上,直线MN经过点(1,0)且垂直于x轴,若△A1B1C1和△ABC关于直线MN成轴对称
已知△ABC在平面直角坐标系中的位置如图所示,每个小正方形的边长为1,点ABC都在格点上,直线MN经过点(1,0)且垂直于x轴,若△A1B1C1和△ABC关于直线MN成轴对称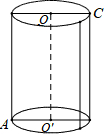 如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)
如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)