题目内容
3.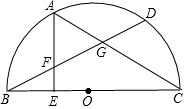 已知:如图,BC是半⊙O的直径,点D在半⊙O,上点A是弧BD的中点.AE⊥BC,垂足为E,BD分别交AE,AC于点F,G.
已知:如图,BC是半⊙O的直径,点D在半⊙O,上点A是弧BD的中点.AE⊥BC,垂足为E,BD分别交AE,AC于点F,G.(1)求证:AF=BF;
(2)点D在何处时,有AG=FG?指出点D的位置并加以证明.
分析 (1)连接AB,由BC是半⊙O的直径,得到∠BAC=90°,根据余角的性质得到∠BAE=∠C,根据圆周角定理得到∠ABD=∠C,等量代换得到∠ABD=∠BAE,于是得到结论;
(2)根据圆周角定理得到∠C=∠EBF,根据余角的性质得到∠BAE=∠C,等量代换得到∠AFG=∠GAF,于是得到结论.
解答 (1)证明:连接AB,
∵BC是半⊙O的直径,
∴∠BAC=90°,
∴∠C+∠ABC=90°,
∵AE⊥BC,
∴∠BAE+∠ABE=90°,
∴∠BAE=∠C,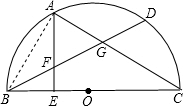
∵点A是弧BD的中点,
∴$\widehat{AB}$=$\widehat{AD}$,
∴∠ABD=∠C,
∴∠ABD=∠BAE,
∴AF=BF;
(2)解:当$\widehat{AB}$=$\widehat{CD}$时,有AG=FG,
∴∠C=∠EBF,
∵∠BAC=∠AEC=90°,
∴∠GAF+∠BAE=∠EAC+∠C=90°,
∴∠BAE=∠C,
∴∠EBF=∠BAE,
∵∠AFG=∠BFE,
∴∠AFG+∠FBE=∠BAF+∠FAG=90°,
∴∠AFG=∠GAF,
∴AG=FG.
点评 本题考查了圆周角定理,直角三角形的性质,等腰三角形的判定,正确的作出辅助线是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
18.实验中学团委举办了“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上获优胜奖,达到9分以上获优秀奖.这次竞赛中初中、高中两组学生成绩分布的条形统计图如下:
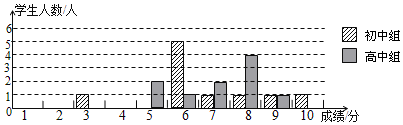
(1)补充完成下列的成绩统计分析表:
(2)安欣同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知:安欣是初中组学生(填“初中”或“高中”);
(3)初中组同学说他们组的优胜奖率、优秀奖率均高于高中组,所以他们组的成绩好于高中组.但高中组同学不同意初中组同学的说法,认为他们组的成绩要好于初中组.请你给出两条支持高中组同学观点的理由.

(1)补充完成下列的成绩统计分析表:
| 组别 | 平均分 | 中位数 | 众数 | 方差 | 优胜奖率 | 优秀奖率 |
| 初中 | 6.7 | 6 | 6 | 3.41 | 90% | 20% |
| 高中 | 7.1 | 7.5 | 8 | 1.69 | 80% | 10% |
(3)初中组同学说他们组的优胜奖率、优秀奖率均高于高中组,所以他们组的成绩好于高中组.但高中组同学不同意初中组同学的说法,认为他们组的成绩要好于初中组.请你给出两条支持高中组同学观点的理由.
15.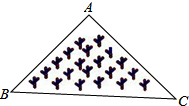 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )| A. | △ABC三边的垂直平分线的交点 | B. | △ABC的三条中线的交点 | ||
| C. | △ABC三条角平分线的交点 | D. | △ABC三条高所在直线的交点 |
13.已知代数式2x+y的值是3,则代数式8x+4y+1的值是( )
| A. | 1 | B. | 4 | C. | 13 | D. | 不能确定 |
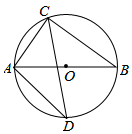 如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.
如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB. 如图,△ABC中,∠CAB的平分线与BC的垂直平分线相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.
如图,△ABC中,∠CAB的平分线与BC的垂直平分线相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.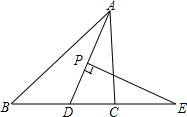 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E