题目内容
17.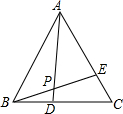 如图,已知等边△ABC中,DC=EA,AD与BE相交于点P,求∠APB的度数.
如图,已知等边△ABC中,DC=EA,AD与BE相交于点P,求∠APB的度数.
分析 易证△BEA≌△ADC,即可求得∠ABE=∠CAD,根据三角形内角和为180°即可解题.
解答 解:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠ACD=60°,
在△BEA和△ADC中,$\left\{\begin{array}{l}{DC=BA}&{\;}\\{∠BAE=∠ACD}&{\;}\\{AB=AC}&{\;}\end{array}\right.$
∴△BEA≌△ADC,(SAS)
∴∠ABE=∠CAD,
∵∠APB=180°-∠BAD-∠ABP,
∴∠APB=180°-∠CBP-∠ABP=180°-∠BAC=120°.
点评 本题考查了等边三角形的性质、全等三角形的判定和性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
5.已知a,b,c是△ABC的三条边,若方程(c-b)x2+2(b-a)x+a-b=0有两个相等实数根,那么,这个三角形是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
6.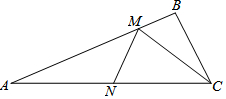 如图:△ABC中,AC=$\sqrt{6}$,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=$\sqrt{6}$,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
 如图:△ABC中,AC=$\sqrt{6}$,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=$\sqrt{6}$,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 3 |
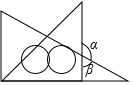 如果我们将一副三角尺按如图所示的位置摆放,并且已知∠a=118°28',那么∠B的度数为61°32'.
如果我们将一副三角尺按如图所示的位置摆放,并且已知∠a=118°28',那么∠B的度数为61°32'. 如图,△ABC中,∠CAB的平分线与BC的垂直平分线相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.
如图,△ABC中,∠CAB的平分线与BC的垂直平分线相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.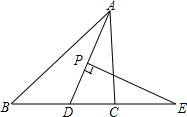 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E 如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2cm,OA=60cm,OB=15cm,则火焰AC的长度为8cm.
如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2cm,OA=60cm,OB=15cm,则火焰AC的长度为8cm.