题目内容
6.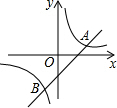 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1)(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
分析 (1)把A点的坐标代入反比例函数y=$\frac{k}{x}$的解析式,即可求得k的值,得出A的坐标,然后代入一次函数的解析式,即可求得b的值;
(2)联立方程即可求得交点B的坐标,根据图象和交点坐标求得x的取值范围即可.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1),
∴1=$\frac{k}{-k+4}$,解得k=2,
∴A(2,1),反比例函数表达式y=$\frac{2}{x}$,
把A(2,1)代入y=x+b得,1=2+b,解得b=-1,
一次函数的表达式为y=x-1;
(2)解$\left\{\begin{array}{l}{y=x-1}\\{y=\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
∴B点的坐标为(-1,-2),
由图象可知,当一次函数的值小于反比例函数的值时,
x的取值范围是x<-1或0<x<2.
点评 本题考查了待定系数法求反比例函数和一次函数的解析式以及反比例函数和一次函数的交点,本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若a为方程x2+2x-5=0的解,则3a2+6a+1的值为( )
| A. | 12 | B. | 16 | C. | 9 | D. | 6 |
 如图,公路PQ和公路MN交于点P,且∠NPQ=30°,公路PQ上有一所学校A,AP=160米.若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响,假设拖拉机行驶时周围100米以内会受到噪声的影响;则造成影响的时间为$\frac{20}{3}$秒.
如图,公路PQ和公路MN交于点P,且∠NPQ=30°,公路PQ上有一所学校A,AP=160米.若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响,假设拖拉机行驶时周围100米以内会受到噪声的影响;则造成影响的时间为$\frac{20}{3}$秒.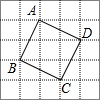 在如图的5×5网格中,小方格的边长为1.
在如图的5×5网格中,小方格的边长为1.
 如图,AB是⊙O的弦,D、E是⊙O上任意两点,连接AD,DE,AE与BD相交于点C,现给出下列四个条件:①∠ACD=∠DAB; ②AD=DE;③AD2=BD•CD; ④AD•AB=AC•BD.在以上4个条件中选取一个,能使△DAC∽△DBA的选法有( )
如图,AB是⊙O的弦,D、E是⊙O上任意两点,连接AD,DE,AE与BD相交于点C,现给出下列四个条件:①∠ACD=∠DAB; ②AD=DE;③AD2=BD•CD; ④AD•AB=AC•BD.在以上4个条件中选取一个,能使△DAC∽△DBA的选法有( )