题目内容
19.在4点至5点之间,从四点钟整起,再经过$\frac{60}{11}$或$\frac{420}{11}$分钟后,时针与分针夹角为90°.分析 分针每分钟走:360÷60=6度,时钟每小时走360÷12=30度,每分钟走30÷60=0.5度,再分分针在时针的后面与分针在时针的前面两种情况列出方程求解即可.
解答 解:设在4点x分时,时针与分针夹角为90°.
此时,分针与0分的夹角为6x度,时针与0时的夹角为(4×30+0.5x)度
有两种情况:
分针在时针的后面时,4×30+0.5x-6x=90,
解得x=$\frac{60}{11}$;
当分针在时针的前面时,6x-(4×30+0.5x)=90,
解得x=$\frac{420}{11}$.
答:再经过$\frac{60}{11}$或$\frac{420}{11}$分钟后,时针与分针夹角为90°.
故答案为$\frac{60}{11}$或$\frac{420}{11}$.
点评 本题考查钟表时针与分针的夹角及一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列各组长度的线段能构成三角形的是( )
| A. | 1.5cm,3.9cm,2.3cm | B. | 3.5cm,7.1cm,3.6cm | ||
| C. | 6cm,1cm,6cm | D. | 4cm,10cm,4cm |
11.下列图形具有稳定性的是( )
| A. | 三角形 | B. | 梯形 | C. | 长方形 | D. | 正方形 |
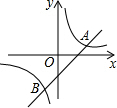 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1) 如图,△DEF是由△ABC绕某点旋转得到,请画出这两个图形的对称中心(不写作法).
如图,△DEF是由△ABC绕某点旋转得到,请画出这两个图形的对称中心(不写作法).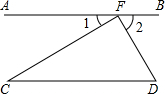 如图,CF⊥DF,且∠1与∠D互余.
如图,CF⊥DF,且∠1与∠D互余.