��Ŀ����
1����ͼ1��ƽ��ֱ������ϵxOy�У���D��-4��0����OC=8����������y=$\frac{1}{3}$x2ƽ�ƺ�C��D���㣬�õ�ͼ1�е�������W��
��1����������W�ı���ʽ��������W��x����һ������A�����ꣻ
��2����ͼ2����OA��OCΪ��������OABC������OB��������OABC��O�����������OB���������˶����ٶ�Ϊÿ��1����λ�õ�����O��A��B��C�䣬��O������������W��ʱ���ε��˶�ʱ�䣻
��3���ڣ�2���������£���ͼ3�����δ�O�������ͬʱ����P��A������ؾ��εı�A��B���B��C����ÿ��$\frac{2}{5}$����λ���ٶ������˶�������P����C��ʱ�����κ͵�Pͬʱֹͣ�˶������˶�ʱ��Ϊt�룮
�����ú�t�Ĵ���ʽ��ʾ��P�����ꣻ
����֪����P�ڱ�A��B�����˶�ʱ��������·����һ���߶Σ����P�ڱ�A��B�����˶�������ʱ����D��CP�ľ������
���� ��1��������ã�D��-4��0����C��0��-8�������ݴ���ϵ��������������w�Ľ���ʽ����һ���õ�������w����һ���㣻
��2���ⷨһ�������⣺���˶������У�����t���O�������Ϊ����$\frac{3}{5}$t��-$\frac{4}{5}$t������O�����y=$\frac{1}{3}$��x-1��2-8$\frac{1}{3}$���ⷽ�̼�����⣻
�ⷨ��������OB�����ʽΪ��y=-$\frac{4}{3}$x������������w�Ľ���ʽ���ⷽ���鼴����⣻
��3������P��x��y�����������������I����0��t��20ʱ������P��A��B����ϣ���II����20��t��35ʱ������P��B��C����ϣ�������B��㣩���������ۼ�����⣻
�ڷ��������������P��A��B���˶�ʱ��0��t��20����CP��APʱ��CPȡ����Сֵ���������ۼ�����⣮
��� �⣺��1��������ã�D��-4��0����C��0��-8����
��������w�Ľ���ʽΪy=$\frac{1}{3}$��x+m��2+n����
$\left\{\begin{array}{l}{\frac{1}{3}��-4+m��^{2}+n=0}\\{\frac{1}{3}{m}^{2}+n=-8}\end{array}\right.$��
���m=-1��n=-8$\frac{1}{3}$��
��������w�Ľ���ʽΪ��y=$\frac{1}{3}$��x-1��2-8$\frac{1}{3}$��
��һ����Ϊ��1+1-��-4����0��������6��0����
��2���ⷨһ�������⣺���˶������У�
����t���O�����������$\frac{3}{5}$t��-$\frac{4}{5}$t����
��O�����y=$\frac{1}{3}$��x-1��2-8$\frac{1}{3}$��
��ȥ��ֵ�ã�t=$\frac{20}{3}$��
����$\frac{20}{3}$��O������������w�ϣ�
�ⷨ��������OB�����ʽΪ��y=-$\frac{4}{3}$x��
��$\left\{\begin{array}{l}{y=-\frac{4}{3}x}\\{y=\frac{1}{3}{x}^{2}-\frac{2}{3}x-8}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=4}\\{y=-\frac{16}{3}}\end{array}\right.$��
��O�䣨4��-$\frac{16}{3}$����
��OO��=$\sqrt{{4}^{2}+��\frac{16}{3}��^{2}}$=$\frac{20}{3}$��
�ྭ��$\frac{20}{3}$��O������������W�ϣ�
��3������P��x��y����
��I����0��t��20ʱ������P��A��B����ϣ�A��P=$\frac{2}{5}$t��A�䣨6+$\frac{3}{5}$t��-$\frac{4}{5}$t����
��x=6+$\frac{3}{5}$t��y=-$\frac{6}{5}$t��
��II����20��t��35ʱ������P��B��C����ϣ�������B��㣩��
B��P=$\frac{2}{5}$t-8��B�䣨6+$\frac{3}{5}$t��-8-$\frac{4}{5}$t����
��x=$\frac{1}{5}$t+14��y=-8-$\frac{4}{5}$t��
������������0��t��20ʱ��P��6+$\frac{3}{5}$t��-$\frac{6}{5}$t������20��t��35ʱ��P��$\frac{1}{5}$t+14��-8-$\frac{4}{5}$t����
����ͼ��
����P��A��B���˶�ʱ��0��t��20��
��P��������·�����ں�������ʽΪ��y=-2x+12��
�֡�ֱ��CD����ʽΪ��y=-2x+8��
��DC��AP��
���DCP���Ϊ��ֵ��
��CPȡ����Сֵʱ����D��CP�ľ������
��ͼ��
��CP��APʱ��CPȡ����Сֵ
����P��PM��y���ڵ�M�����PMC=90��
��P��6+$\frac{3}{5}$t��-$\frac{6}{5}$t����
��CM=8-$\frac{6}{5}$t��PM=6+$\frac{3}{5}$t��
�ߡ�DCO+��PCM=90�㣬
��CPM+��PCM=90��
���CPM=��DCO��
��tan��CPM=tan��DCO=$\frac{1}{2}$��
��Rt��PMC����PMC=90��
��PM=2CM��
��t=$\frac{10}{3}$��
���飺0��$\frac{10}{3}$��20��
�ྭ��$\frac{10}{3}$��ʱ����D��CP�ľ������
���� ���⿼���������߽���ʽ��ȷ�������ε����ʡ�����˼�����Ҫ֪ʶ�㣬��3���٢�С���У����õ��˷������۵���ѧ˼�룬�ѵ����ڿ�������Ҫȫ�棬�������ز�©��

 ��ͼ��ʾ��ijͬѧ��һ�������εIJ�������������飬����Ҫ��������ȥ��һ����ȫһ���IJ�������ô��ʡ�µİ취�Ǵ��ڢۿ�ȥ��������ţ�
��ͼ��ʾ��ijͬѧ��һ�������εIJ�������������飬����Ҫ��������ȥ��һ����ȫһ���IJ�������ô��ʡ�µİ취�Ǵ��ڢۿ�ȥ��������ţ� | A�� | 520̨ | B�� | 550̨ | C�� | 600̨ | D�� | 620̨ |
| A�� | ������ | B�� | ���� | C�� | ������ | D�� | ������ |
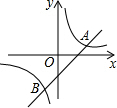 ��ͼ����֪����������y=$\frac{k}{x}$��һ�κ���y=x+b��ͼ���ڵ�һ�����ཻ�ڵ�A��-k+4��1��
��ͼ����֪����������y=$\frac{k}{x}$��һ�κ���y=x+b��ͼ���ڵ�һ�����ཻ�ڵ�A��-k+4��1��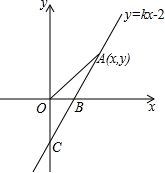 ��ͼ��ֱ��y=kx-2��x�ᡢy��ֱ���B��C���㣬OB��OC=$\frac{1}{2}$��
��ͼ��ֱ��y=kx-2��x�ᡢy��ֱ���B��C���㣬OB��OC=$\frac{1}{2}$�� ��ͼ����DEF���ɡ�ABC��ij����ת�õ����뻭��������ͼ�εĶԳ����ģ���д��������
��ͼ����DEF���ɡ�ABC��ij����ת�õ����뻭��������ͼ�εĶԳ����ģ���д��������