题目内容
11.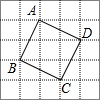 在如图的5×5网格中,小方格的边长为1.
在如图的5×5网格中,小方格的边长为1.(1)图中格点正方形ABCD的面积为5;
(2)若连接AC,则以AC为一边的正方形的面积为10;
(3)在所给网格中画一个格点正方形,使其各边都不在格线上且面积最大,你所画的正方形面积为17.
分析 (1)先根据勾股定理求出AB的长,再由正方形的面积公式即可得出结论;
(2)先根据勾股定理求出AC的长,再由正方形的面积公式即可得出结论;
(3)画出符合条件的正方形,再求出其面积即可.
解答 解:(1)∵AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴S正方形ABCD=5.
故答案为:5;
(2)∵正方形ABCD的边长为$\sqrt{5}$,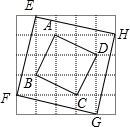
∴AC=$\sqrt{{(\sqrt{5})}^{2}+{(\sqrt{5})}^{2}}$=$\sqrt{10}$,
∴以AC为一边的正方形的面积=10.
故答案为:10;
(3)如图,S正方形EFGH=($\sqrt{17}$)2=17.
故答案为:17.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
2.在平面直角坐标系中,抛物线y=ax2-4ax+4a+c与x轴交于点A和点B,与y轴的负半轴交于点C,点A的坐标为(1,0),OB=OC.
(1)求点C的坐标.
(2)求抛物线的顶点P到直线BC的距离.
(1)求点C的坐标.
(2)求抛物线的顶点P到直线BC的距离.
4.下列各组长度的线段能构成三角形的是( )
| A. | 1.5cm,3.9cm,2.3cm | B. | 3.5cm,7.1cm,3.6cm | ||
| C. | 6cm,1cm,6cm | D. | 4cm,10cm,4cm |
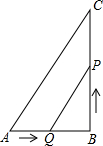 如图所示,已知在△ABC中,∠B=90°,AB=6cm,BC=12cm,点Q从点A开始沿 AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动.
如图所示,已知在△ABC中,∠B=90°,AB=6cm,BC=12cm,点Q从点A开始沿 AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动.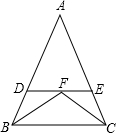 阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边”,如图,在△ABC中,已知∠ABC和∠ACB的平分线上交于点F,过点F作BC的平行线分别交AB、AC于点D、E,
阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边”,如图,在△ABC中,已知∠ABC和∠ACB的平分线上交于点F,过点F作BC的平行线分别交AB、AC于点D、E,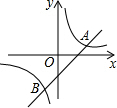 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1)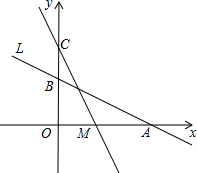 如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.