题目内容
18. 如图,AB是⊙O的弦,D、E是⊙O上任意两点,连接AD,DE,AE与BD相交于点C,现给出下列四个条件:①∠ACD=∠DAB; ②AD=DE;③AD2=BD•CD; ④AD•AB=AC•BD.在以上4个条件中选取一个,能使△DAC∽△DBA的选法有( )
如图,AB是⊙O的弦,D、E是⊙O上任意两点,连接AD,DE,AE与BD相交于点C,现给出下列四个条件:①∠ACD=∠DAB; ②AD=DE;③AD2=BD•CD; ④AD•AB=AC•BD.在以上4个条件中选取一个,能使△DAC∽△DBA的选法有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
分析 根据两边对应成比例且夹角相等的两个三角形相似,可判断③④;根据两个角对应相等的两个三角形相似,可判断①②.
解答 解:①∠ACD=∠DAB,∠ADC=∠BDA,△ADC与△ABD相似,故①正确;
②由AD=DE,得∠DAC=∠DBA,又∵∠ADC=∠BDA,△ADC与△ABD相似,故②正确;
③由AD2=BD•CD,得AB:BD=CD:BD,且∠ADC=∠BDA,△ADC∽△BDA,故③正确;
④由AD•AB=AC•BD,则AD:BD=AB:AC,而∠DAC=∠DBA不一定成立,所以△ADC与△ABD不一定相似故④不正确,
所以4个条件中选取一个,能使△DAC∽△DBA的选法有3个.
故选C.
点评 本题考查了相似三角形的判定与性质,利用了相似三角形的判定:两边对应成比例且夹角相等的两个三角形相似;两个角对应相等的两个三角形相似,解题的关键是熟记相似三角形的各种判定方法及其性质.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
13.某工厂计划生产500台电视机,实际增产$\frac{1}{5}$,实际生产电视机( )
| A. | 520台 | B. | 550台 | C. | 600台 | D. | 620台 |
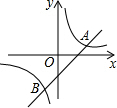 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1)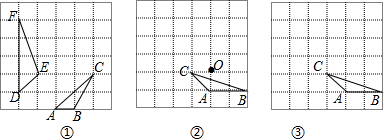
 如图,△DEF是由△ABC绕某点旋转得到,请画出这两个图形的对称中心(不写作法).
如图,△DEF是由△ABC绕某点旋转得到,请画出这两个图形的对称中心(不写作法).