题目内容
4. 如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20 cm,则CQ的长是( )
如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20 cm,则CQ的长是( )| A. | 8 cm | B. | 12 cm | C. | 30 cm | D. | 50 cm |
分析 利用平行线分线段成比例得到$\frac{AB}{AP}$=$\frac{AC}{AQ}$,即$\frac{AC}{20}$=$\frac{2}{5}$,然后利用比例性质求出AC,然后计算CQ.
解答 解:∵BC∥PQ,
∴$\frac{AB}{AP}$=$\frac{AC}{AQ}$,即$\frac{AC}{20}$=$\frac{2}{5}$,
∴AC=8,
∴CQ=AQ-AC=20-8=12(cm).
故选B.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施,假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1 250元,衬衫的单价降了x元,那么下面所列的方程正确的是( )
| A. | (20+x)(40-2x)=1250 | B. | (20+x)(40-x)=1250 | C. | (20+2x)(40-2x)=1250 | D. | (20+2x)(40-x)=1250 |
16.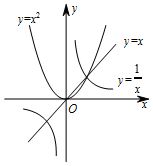 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a时,那么a<-1.
则( )
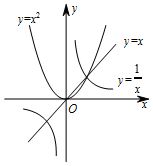 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a时,那么a<-1.
则( )
| A. | 正确的命题是①④ | B. | 错误的命题是②③④ | C. | 正确的命题是①② | D. | 错误的命题只有③ |
14.下列算式中,正确的是( )
| A. | 2x+2y=4xy | B. | 2a2+2a3=2a5 | C. | 4a2-3a2=1 | D. | -2ba2+a2b=-a2b |
 如图,I为△ABC的角平分线交点,∠A=40°,则∠BIC的度数是110°.
如图,I为△ABC的角平分线交点,∠A=40°,则∠BIC的度数是110°.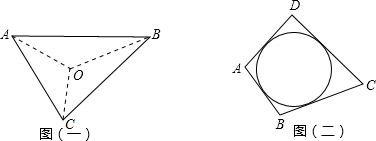
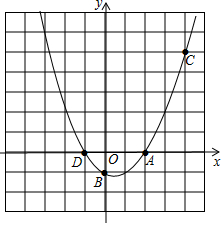 如图,已知二次函数y=ax2+bx+c经过点A(2,0),B(0,-1),C(4,5)三点.
如图,已知二次函数y=ax2+bx+c经过点A(2,0),B(0,-1),C(4,5)三点. 如图,A、O、B在同一条直线上,如果OA的方向是北偏西25°那么OB的方向是南偏东25°.
如图,A、O、B在同一条直线上,如果OA的方向是北偏西25°那么OB的方向是南偏东25°.