题目内容
5.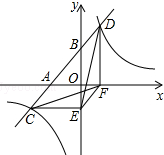 如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=$\frac{k}{x}$相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=$\frac{k}{x}$相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 设D(x,$\frac{k}{x}$),得出F(x,0),根据三角形的面积求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据全等三角形的判定判断②即可;证出平行四边形BDFE和平行四边形ACEF,得到BD=AC即可.
解答 解:①设D(x,$\frac{k}{x}$),则F(x,0),
由图象可知x>0,k>0,
∴△DEF的面积是$\frac{1}{2}$×$\frac{k}{x}$×x=$\frac{1}{2}$k,
同理可知:△CEF的面积是$\frac{1}{2}$k,
∴△CEF的面积等于△DEF的面积,
∴①正确;
②条件不足,无法证出两三角形全等的条件,
∴②错误;
③∵△CEF的面积等于△DEF的面积,
∴边EF上的高相等,
∴CD∥EF,
∵BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
同理EF=AC,
∴AC=BD,
∴③正确;正确的有2个.
故选:C.
点评 本题考查了平行四边形的性质和判定,三角形的面积,全等三角形的判定,相似三角形的判定等知识点的运用,关键是检查学生综合运用定理进行推理的能力,题目具有一定的代表性,有一定的难度,是一道比较容易出错的题目.

练习册系列答案
相关题目
16.[x]表示不超过实数x的最大整数(如[π]=3,[-π]=-4,[-4]=-4,记M=[x]+[2x]+[3x]将不能表示成M形式的正整数称为“隐形数”.则不超过2014的“隐形数”的个数是( )
| A. | 335 | B. | 336 | C. | 670 | D. | 671 |
10.若关于x的不等式$\frac{2x+3}{2}$>2x+$\frac{m}{2}$的正整数解为1,2,3,则m的取值范围( )
| A. | -7<m≤-5 | B. | -7≤m<-5 | C. | -5<m≤-3 | D. | -5≤m<-3 |
 如图,在平面直角坐标系xOy中,双曲线y1=$\frac{2}{x}$
如图,在平面直角坐标系xOy中,双曲线y1=$\frac{2}{x}$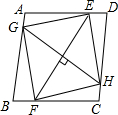 如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形.
如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形. 如图,AB=DC.
如图,AB=DC. 如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=6cm,BC=10cm,动点P、Q分别从A、C同时出发,点P以1cm/秒的速度由A向D运动,点Q以2cm/秒的速度由C向B运动,其中一动点达到端点时,另一动点随之停止运动.
如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=6cm,BC=10cm,动点P、Q分别从A、C同时出发,点P以1cm/秒的速度由A向D运动,点Q以2cm/秒的速度由C向B运动,其中一动点达到端点时,另一动点随之停止运动.