题目内容
18.如图(1),点P、Q分别在x轴、y轴上.
(1)已知点P(3,0),Q(0,4),点M在线段PQ上,直线OM把△POQ分成两个三角形,且这两个三角形的面积的比是2:1.求直线OM的函数解析式;
(2)如图(2),已知P(m,0),Q(0,n)(m>0,n>0),反比例函数y=$\frac{m}{x}$的图象与线段PQ交于C、D两点,若S△POC=S△COD=S△DOQ,求n的值.
分析 (1)设点M的坐标为(x,y),根据点P、Q的坐标结合三角形的面积公式可得出点M的坐标,由此即可得出结论;
(2)过点D作DE⊥x轴于点E,过点C作CF⊥x轴于点F.由S△POC=S△COD=S△DOQ可得出PC=CD=DQ,即OE=EF=FP,再根据P点的坐标即可得出“OE=$\frac{1}{3}$m,OF=$\frac{2}{3}$m”,设直线PQ的解析式为y=kx+n,由点P(m,0)结合待定系数法求函数解析式即可得出直线PQ的解析式,将反比例函数解析式代入直线解析式中,由根与系数的关系可表示出x1•x2,结合OE=$\frac{1}{3}$m、OF=$\frac{2}{3}$m即可求出n的值.
解答 解:(1)结合题意画出图形,如图(1)所示.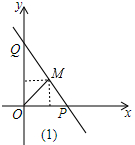
设点M的坐标为(x,y).
则S△POM=$\frac{1}{2}$y•OP,S△QOM=$\frac{1}{2}$x•OQ.
点P(3,0),Q(0,4),
∴OP=3,OQ=4.
当S△POM:S△QOM=1:2时,有6y=4x,
∴此时直线OM的函数解析式为y=$\frac{2}{3}$x;
当S△POM:S△QOM=2:1时,有3y=8x,
∴此时直线OM的函数解析式为y=$\frac{8}{3}$x.
综上知:直线OM的函数解析式为y=$\frac{2}{3}$x或y=$\frac{8}{3}$x.
(2)过点D作DE⊥x轴于点E,过点C作CF⊥x轴于点F,如图2所示.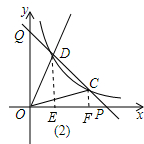
∵S△POC=S△COD=S△DOQ,
∴PC=CD=DQ,即OE=EF=FP,
∵OP=3OE=m,
∴OE=$\frac{1}{3}$m,OF=$\frac{2}{3}$m.
设直线PQ的解析式为y=kx+n,
∵点P(m,0)在直线PQ上,
∴0=km+n,解得:k=-$\frac{n}{m}$,
即直线PQ的解析式为y=-$\frac{n}{m}$x+n.
令-$\frac{n}{m}$x+n=$\frac{m}{x}$,即nx2-mnx+m2=0,
则x1•x2=OE•OF=$\frac{{m}^{2}}{n}$=$\frac{1}{3}$m×$\frac{2}{3}$m,
解得:n=$\frac{9}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及三角形的面积公式,解题的关键:(1)结合三角形的面积公式找出点M的坐标;(2)结合根与系数的关系找出关于n的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据三角形的面积公式求出点的坐标,再由点的坐标结合待定系数法求出函数解析式是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
| A. | -7<m≤-5 | B. | -7≤m<-5 | C. | -5<m≤-3 | D. | -5≤m<-3 |
| 年龄 | 28≤X<30 | 30≤X<32 | 32≤X<34 | 34≤X<36 | 36≤X<38 | 38≤X<40 | 40≤X<42 |
| 频数 | 4 | 3 | 8 | 7 | 9 | 11 | 2 |
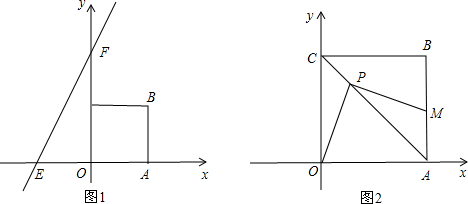
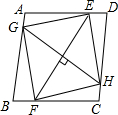 如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形.
如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形. 如图,在平行四边形ABCD中,DE⊥AB于E,BM=MC=DC,那么∠EMC与∠BEM的大小关系怎样?
如图,在平行四边形ABCD中,DE⊥AB于E,BM=MC=DC,那么∠EMC与∠BEM的大小关系怎样?