题目内容
如图，王老师站在湖边度假村的景点A处，观察到一只水鸟由岸边D处飞向湖中小岛C处，点A到DC所在水平面的距离AB是15米，观测水鸟在点D和点C处时的俯角分别为53°和11°，求C、D两点之间距离．（精确到0.1．参考数据sin53°≈0.80，cos53°≈0.60，tan53°≈1.33，sin11°≈0.19，cos11°≈0.98，tan11°≈0.19）考点：解直角三角形的应用-仰角俯角问题
专题：计算题
分析：根据AB=15米，点D和点C处时的俯角分别为53°和11°，在Rt△ABD和Rt△ABC中，分别求出BC和BD的长度，然后即可求出CD=BC-CD的值．
解答：解：在Rt△ABD中，
∵AB=15米，∠ADB=53°，
∴
=tan53°≈1.33，
∴BD=11.28（米），
在Rt△ABC中，
∵AB=15米，∠ACD=11°，
∴
=tan11°≈0.19，
解得：BC≈78.95（米），
∴CD=BC-BD=78.95-11.28≈67.8（米）．
答：C、D两点之间距离为67.8米．
∵AB=15米，∠ADB=53°，
∴
| AB |
| BD |
∴BD=11.28（米），
在Rt△ABC中，
∵AB=15米，∠ACD=11°，
∴
| AB |
| BC |
解得：BC≈78.95（米），
∴CD=BC-BD=78.95-11.28≈67.8（米）．
答：C、D两点之间距离为67.8米．
点评：本题考查了解直角三角形的应用，解答本题的关键是根据俯角构造直角三角形，利用三角函数的知识求解．
练习册系列答案
相关题目
将一副三角尺如图放置，则∠APD=
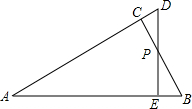把两个一样的直角三角板的30°角重合，其两对边交于点P（如图），连接BD，下列说法错误的是（ ）| A、整个图形是轴对称图形 |
| B、△PEB周长大于DB |
| C、有4对全等三角形（不添线） |
| D、∠EDB=15° |
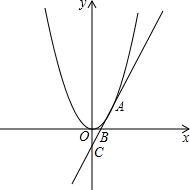已知直线y1=2x-1分别交x轴、y轴于B、C，抛物线y2=mx2过直线y1=2x-1上点A（1，n）．
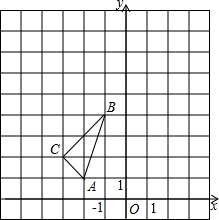如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，1），B（-1，4），C（-3，2）．
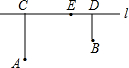如图，在铁路L的同侧有A、B两村庄，已知A庄到L的距离AC=15km，B庄到L的距离BO=l0km，CD=25km．现要在铁路L上建一个土特产收购站E，使得A、B两村庄到E站的距离相等，