题目内容
将一副三角尺如图放置，则∠APD=考点：三角形的外角性质
专题：
分析：根据角度的和差首先求得∠ACP的度数，然后根据∠APD是△ACP的外角，根据三角形的外角的性质求解．
解答：解：∠ACP=∠ACB-∠DCB=90°-45°=45°，
则∠APD=∠A+∠ACP=30°+45°=75°．
故答案是：75°．
则∠APD=∠A+∠ACP=30°+45°=75°．
故答案是：75°．
点评：本题比较简单，考查的是三角形外角的性质：三角形的外角等于两个不相邻的内角的和．
练习册系列答案
相关题目
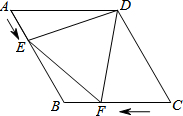如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为
如图，菱形ABCD中，AC∥x轴，点A在反比例函数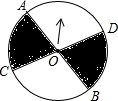
如图，同行转盘中，AB，CD都是直径，圆心角∠AOC=80°，任意旋转这个转盘1次，当旋转停止时，指针指向阴影区域的概率是
如图，Rt△ABC中，∠ACB=90°，∠A=30°，AB=1，过点C作CD⊥AB于点D，过点D作DE∥BC交AC于点E，过点E作EF∥CD交AB于点F，过点F作FG∥BC交AC于点G，…若BC、CD、DE、EF、…的长分别是a1、a2、a3、a4…，猜测an=
如图，一个正方体和一个圆柱体紧靠在一起，其左视图是（ ）A、 |
B、 |
C、 |
D、 |
把球放在长方体纸盒内，球的一部分露出盒外，其截面如图，已知EF=4| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，王老师站在湖边度假村的景点A处，观察到一只水鸟由岸边D处飞向湖中小岛C处，点A到DC所在水平面的距离AB是15米，观测水鸟在点D和点C处时的俯角分别为53°和11°，求C、D两点之间距离．（精确到0.1．参考数据sin53°≈0.80，cos53°≈0.60，tan53°≈1.33，sin11°≈0.19，cos11°≈0.98，tan11°≈0.19）