题目内容
16.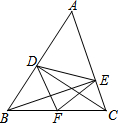 如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长是( )
如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长是( )| A. | 21 | B. | 18 | C. | 13 | D. | 15 |
分析 根据直角三角形斜边上的中线等于斜边的一半求出DF、EF,再根据三角形的周长的定义解答.
解答 解:∵CD⊥AB,F为BC的中点,
∴DF=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
∵BE⊥AC,F为BC的中点,
∴EF=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
∴△DEF的周长=DE+EF+DF=5+4+4=13.
故选C.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,是基础题,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
6.同时经过平面三点可确定的直线的条数是( )
| A. | 0 | B. | 0或1 | C. | 1或3 | D. | 3 |
7.下列方程是一元二次方程的是( )
| A. | ax2-2x+=0(a是已知数) | B. | 3x2+2x-4=3x2 | ||
| C. | 5x2-2x=0 | D. | $\frac{{x}^{3}+2x}{x}$=1 |
4.等腰三角形的两边分别为12和6,则这个三角形的周长是( )
| A. | 24 | B. | 18 | C. | 30 | D. | 24或30 |
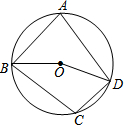 如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD=100°.
如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD=100°.