题目内容
6.已知y1=$\frac{b}{4}$x-4,y2=2ax+4a-b.(1)a,b为何值时,两函数的图象重合?
(2)如果两直线相交于点(-1,3),求a,b的值.
分析 (1)因为两函数的图象重合,也就是两个函数的比例系数与常数项相等,由此建立关于a、b的方程组,求得a、b的数值;
(2)根据两直线相交于点(-1,3),把x=-1,y=3代入两个函数,得到关于a、b的方程组,再解方程组即可.
解答 解:(1)∵y1=$\frac{b}{4}$x-4,y2=2ax+4a-b的图象重合,
∴$\left\{\begin{array}{l}{\frac{b}{4}=2a}\\{4a-b=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=8}\end{array}\right.$;
(2)∵两直线相交于点(-1,3),
∴$\left\{\begin{array}{l}{3=-\frac{b}{4}-4}\\{3=-2a+4a-b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{25}{2}}\\{b=-28}\end{array}\right.$.
点评 本题考查了两条直线相交和平行问题,利用两个一次函数的交点坐标为两函数解析式所组成的方程组的解解决问题.

练习册系列答案
相关题目
16.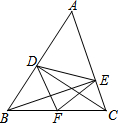 如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长是( )
如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长是( )
 如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长是( )
如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长是( )| A. | 21 | B. | 18 | C. | 13 | D. | 15 |
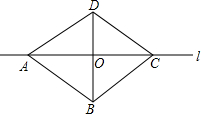 如图所示,直线l是四边形ABCD的对称轴,若AB=CD,有下面4个结论:
如图所示,直线l是四边形ABCD的对称轴,若AB=CD,有下面4个结论: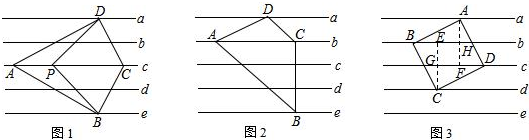
 如图,△ABC被分成了六部分,已知2BD=DC,EC=2AE,△AFO的面积为3平方厘米,则其它5部分的面积各是多少?
如图,△ABC被分成了六部分,已知2BD=DC,EC=2AE,△AFO的面积为3平方厘米,则其它5部分的面积各是多少?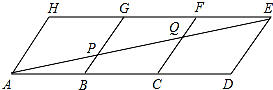 如图,用三个全等的平行四边形ABGH,BCFG,CDEF拼成平行四边形ADEH,连结AE与BG,CF分别交于点P、Q.
如图,用三个全等的平行四边形ABGH,BCFG,CDEF拼成平行四边形ADEH,连结AE与BG,CF分别交于点P、Q.