题目内容
8．现有四张分别写有数字1，2，3，4的卡片，它们除数字外完全相同，把卡片背面朝上洗匀，从中随机抽取一张不放回，再从中随机抽取另一张，若把第一张卡片上的数字作为个位数字，第二张卡片上的数字作为十位数字，组成一个两位数，则这个两位数是3的整数倍的概率是$\frac{1}{3}$．分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与这个两位数是3的整数倍的情况，再利用概率公式即可求得答案．
解答 解：画树状图得：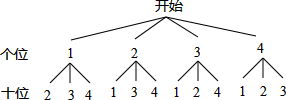
∵共有12种等可能的结果，这个两位数是3的整数倍的有4种情况，
∴这个两位数是3的整数倍的概率是：$\frac{4}{12}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
1．
已知二次函数y=ax2+bx+c（a≠0）的顶点坐标是（-1，-5.2）及部分图象（如图），由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1，x2，若x1=1.3，则x2的值为（ ）
已知二次函数y=ax2+bx+c（a≠0）的顶点坐标是（-1，-5.2）及部分图象（如图），由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1，x2，若x1=1.3，则x2的值为（ ）| A． | -1.3 | B． | -2.3 | C． | -0.3 | D． | -3.3 |
16．
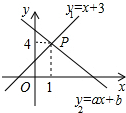如图，一次函数y1=x+3与y2=ax+b的图象相交于点P（1，4），则关于x的不等式x+3≤ax+b的解集是（ ）
如图，一次函数y1=x+3与y2=ax+b的图象相交于点P（1，4），则关于x的不等式x+3≤ax+b的解集是（ ）| A． | x≥4 | B． | x≤4 | C． | x≥1 | D． | x≤1 |
13．在平面直角坐标系中，将点P（a，b）关于原点对称得到点P1，再将点P1向左平移2个单位长度得到点P2，则点P2的坐标是（ ）
| A． | （b-2，-a） | B． | （b+2，-a） | C． | （-a+2，-b） | D． | （-a-2，-b） |
17．人工智能AlphaGo因在人机大战中大胜韩国围棋手李世石九段而声名显赫．它具有自我对弈学习能力，决战前已做了两千万局的训练（等同于一个人近千年的训练量）．此处“两千万”用科学记数法表示为（ ）
| A． | 0.2×107 | B． | 2×107 | C． | 0.2×108 | D． | 2×108 |