题目内容
 如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数.
如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数.考点:等腰三角形的性质
专题:
分析:根据等腰三角形两底角相等可得∠ABC=∠C,然后利用三角形的内角和等于180°列方程求解即可,再求出∠C,然后根据直角三角形两锐角互余列式计算即可得解.
解答:解:∵AB=AC,
∴∠ABC=∠C,
∵∠A+∠ABC+∠C=180°,
∴∠A+2∠A+2∠A=180°,
解得∠A=36°,
∴∠C=2×36°=72°,
∵BD是AC边上的高,
∴∠DBC=90°-∠C=90°-72°=18°.
∴∠ABC=∠C,
∵∠A+∠ABC+∠C=180°,
∴∠A+2∠A+2∠A=180°,
解得∠A=36°,
∴∠C=2×36°=72°,
∵BD是AC边上的高,
∴∠DBC=90°-∠C=90°-72°=18°.
点评:本题考查了等腰三角形的性质,主要利用了等腰三角形两底角相等,直角三角形两锐角互余的性质,熟记性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
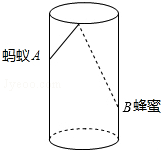 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为 已知AO⊥BO,DO⊥CO,∠AOD=4∠BOC,则∠AOD的度数为
已知AO⊥BO,DO⊥CO,∠AOD=4∠BOC,则∠AOD的度数为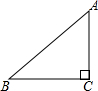 如图,在Rt△ABC中,∠C=90°,AC=6,tanA=
如图,在Rt△ABC中,∠C=90°,AC=6,tanA=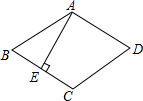 如图,在菱形ABCD中,∠C=120°,AE⊥BC于点E,求证:BE=CE.
如图,在菱形ABCD中,∠C=120°,AE⊥BC于点E,求证:BE=CE.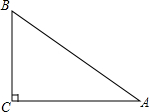 如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用?
如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用?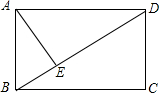 如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6,求矩形ABCD的周长.
如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6,求矩形ABCD的周长. 如图,已知∠1=∠2,∠A=∠D,求证:∠C=∠F.
如图,已知∠1=∠2,∠A=∠D,求证:∠C=∠F.