题目内容
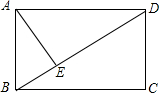 如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6,求矩形ABCD的周长.
如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6,求矩形ABCD的周长.考点:矩形的性质
专题:
分析:由矩形的性质结合条件可证明△ABE∽△DAE,可求得AE,再利用勾股定理可分别求得AB、AD,可求得矩形ABCD的周长.
解答:解:∵四边形ABCD为矩形,
∴∠BAD=90°,
∵AE⊥BD,
∴∠AEB=∠AED=90°,
∴∠ABE+∠BAE=∠BAE+∠DAE,
∴∠ABE=∠DAE,
∴△ABE∽△DAE,
∴
=
,即
=
,解得AE2=12,
在Rt△ABE中,由勾股定理可得AB=
=
=4,
在Rt△ADE中,由勾股定理可得AD=
=
=4
,
故矩形ABCD的周长为2(AB+AD)=2×(4+4
)=8+8
.
∴∠BAD=90°,
∵AE⊥BD,
∴∠AEB=∠AED=90°,
∴∠ABE+∠BAE=∠BAE+∠DAE,
∴∠ABE=∠DAE,
∴△ABE∽△DAE,
∴
| BE |
| AE |
| AE |
| DE |
| 2 |
| AE |
| AE |
| 6 |
在Rt△ABE中,由勾股定理可得AB=
| AE2+BE2 |
| 12+22 |
在Rt△ADE中,由勾股定理可得AD=
| AE2+DE2 |
| 12+62 |
| 3 |
故矩形ABCD的周长为2(AB+AD)=2×(4+4
| 3 |
| 3 |
点评:本题主要考查矩形的性质和相似三角形的判定和性质,利用相似三角形的性质求得AE的长是解题的关键.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、0没有倒数 |
| B、0没有相反数 |
| C、0没有绝对值 |
| D、平方为0的数不存在 |
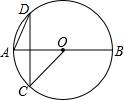 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=70°,则∠BOC=( )
如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=70°,则∠BOC=( )| A、70° | B、130° |
| C、140° | D、160° |
 如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数.
如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数. 如图,已知⊙O中,弦AB的长等于⊙O的半径,求弦所对的圆心角和圆周角的度数.
如图,已知⊙O中,弦AB的长等于⊙O的半径,求弦所对的圆心角和圆周角的度数.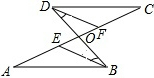 如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD.
如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD. 如图,△ABC中,∠CAB=120°,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF=
如图,△ABC中,∠CAB=120°,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF=