题目内容
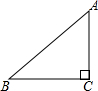 如图,在Rt△ABC中,∠C=90°,AC=6,tanA=
如图,在Rt△ABC中,∠C=90°,AC=6,tanA=| 4 |
| 3 |
考点:锐角三角函数的定义
专题:
分析:根据正切为对边比邻边,可得BC,根据勾股定理,可得AB的长,根据锐角的正弦为对边比斜边,余弦为邻边比斜边,可得答案.
解答:解:由AC=6,tanA=
,得
BC=AC•tanA=
=6×
=8,
由勾股定理,得
AB=
=
=10,
sinA=
=
=
,
cosB=
=
=
.
| 4 |
| 3 |
BC=AC•tanA=
| 4 |
| 3 |
| 4 |
| 3 |
由勾股定理,得
AB=
| BC2+AC2 |
| 62+82 |
sinA=
| BC |
| AB |
| 8 |
| 10 |
| 4 |
| 5 |
cosB=
| BC |
| AB |
| 8 |
| 10 |
| 4 |
| 5 |
点评:本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、0没有倒数 |
| B、0没有相反数 |
| C、0没有绝对值 |
| D、平方为0的数不存在 |
 如图,AB是半圆的直径,AC为弦,OD⊥AB,交AC于点D,垂足为O,⊙O的半径为4,OD=3,求CD的长.
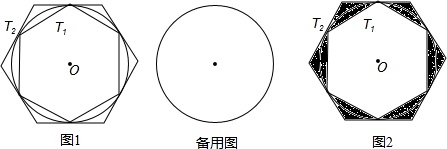
如图,AB是半圆的直径,AC为弦,OD⊥AB,交AC于点D,垂足为O,⊙O的半径为4,OD=3,求CD的长.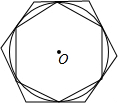 如图,正六边形T1的6个顶点都在⊙O上,正六边形T2的6条边都和⊙O相切(我们称T1、T2分别为⊙O的内接正六边形和外切正六边形)
如图,正六边形T1的6个顶点都在⊙O上,正六边形T2的6条边都和⊙O相切(我们称T1、T2分别为⊙O的内接正六边形和外切正六边形)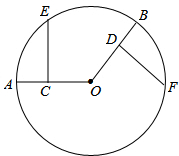 如图,已知AO、BO分别是⊙O的两条半径,C、D分别是AO、BO的中点,CE⊥AO,DF⊥BO.求证:
如图,已知AO、BO分别是⊙O的两条半径,C、D分别是AO、BO的中点,CE⊥AO,DF⊥BO.求证:
 如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数.
如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数. 如图,已知⊙O中,弦AB的长等于⊙O的半径,求弦所对的圆心角和圆周角的度数.
如图,已知⊙O中,弦AB的长等于⊙O的半径,求弦所对的圆心角和圆周角的度数.