题目内容
用一块宽为2m的矩形铁片(如图1),按图中虚线弯折60°角,做成截面为等腰梯形ABCD的水槽(如图2),设腰长AB=x m.
(1)写出用x表示截面ABCD的面积S的表达式;
(2)当腰长x为多少时,横截面积最大?最大面积是多少?
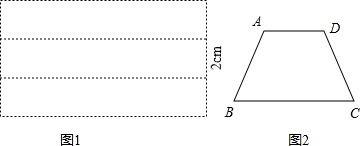
(1)写出用x表示截面ABCD的面积S的表达式;
(2)当腰长x为多少时,横截面积最大?最大面积是多少?
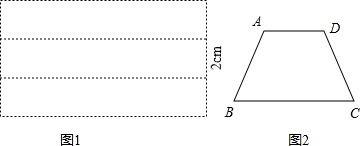
考点:二次函数的应用,等腰梯形的性质
专题:
分析:(1)利用等腰三角形的性质求出AE的长进而得出AD,BC的长即可得出答案;
(2)利用二次函数的最值求出得出答案.
(2)利用二次函数的最值求出得出答案.
解答: 解:(1)过点A作AE⊥BC于点E,
解:(1)过点A作AE⊥BC于点E,
∵∠B=60°,AB=xm,
∴AE=ABsin60°=
x(m),BE=
m,
BC=(2-2x)m,AD=2-2x-
-
=(2-3x)m
故截面ABCD的面积为:
S=
AE×(AD+BC)
=
×
x(2-3x+2-2x)
=
x(4-5x)
=-
x2+
x;
(2)S=-
x2+
x
=-
(x2-
x)
=-
(x2-
x+
-
)
=-
(x-
)2+
即当腰长x为
m时,横截面积最大,最大面积是
m2.
 解:(1)过点A作AE⊥BC于点E,
解:(1)过点A作AE⊥BC于点E,∵∠B=60°,AB=xm,
∴AE=ABsin60°=
| ||
| 2 |
| x |
| 2 |
BC=(2-2x)m,AD=2-2x-
| x |
| 2 |
| x |
| 2 |
故截面ABCD的面积为:
S=
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 4 |
=-
5
| ||
| 4 |
| 3 |
(2)S=-
5
| ||
| 4 |
| 3 |
=-
5
| ||
| 4 |
| 4 |
| 5 |
=-
5
| ||
| 4 |
| 4 |
| 5 |
| 4 |
| 25 |
| 4 |
| 25 |
=-
5
| ||
| 4 |
| 2 |
| 5 |
| ||
| 5 |
即当腰长x为
| 2 |
| 5 |
| ||
| 5 |
点评:此题主要考查了二次函数的应用以及等腰梯形的性质,得出等腰梯形的上底与下底的长是解题关键.

练习册系列答案
相关题目
下列命题中正确的是( )
①三边对应相等的两个三角形全等;
②有两边对应相等的两个直角三角形全等;
③有一边对应相等的两个等腰直角三角形全等;
④有一边重合的两个等腰三角形全等.
①三边对应相等的两个三角形全等;
②有两边对应相等的两个直角三角形全等;
③有一边对应相等的两个等腰直角三角形全等;
④有一边重合的两个等腰三角形全等.
| A、①② | B、①③ |
| C、①②③ | D、①②③④ |
已知静水中航行,甲船的速度比乙船快,在水流速度不为零的河流中,甲、乙两船同时从A港出发,同向航行一小时后立即返航,那么( )
| A、甲船先返回A港 |
| B、乙船先返回A港 |
| C、甲、乙两船同时返回A港 |
| D、不能确定哪条船先返回A港 |
 如图,在平行四边形ABCD中,AB=a,BC=b,∠ABC=β,试用a、b、β表示平行四边形的面积.
如图,在平行四边形ABCD中,AB=a,BC=b,∠ABC=β,试用a、b、β表示平行四边形的面积.