题目内容
下列命题中正确的是( )
①三边对应相等的两个三角形全等;
②有两边对应相等的两个直角三角形全等;
③有一边对应相等的两个等腰直角三角形全等;
④有一边重合的两个等腰三角形全等.
①三边对应相等的两个三角形全等;
②有两边对应相等的两个直角三角形全等;
③有一边对应相等的两个等腰直角三角形全等;
④有一边重合的两个等腰三角形全等.
| A、①② | B、①③ |
| C、①②③ | D、①②③④ |
考点:命题与定理,全等三角形的判定
专题:
分析:根据全等三角形的判定定理分别判断各说法或举出反例即可.
解答:解:①三边对应相等的两个三角形全等即SSS,故原说法正确;
②两边对应相等的两个直角三角形全等,若是两条直角边对应相等,可以根据SAS判定全等,若是直角边与斜边对应相等,可根据HL判定全等.故原说法正确;
如果这两个三角形一个是锐角三角形,一个是钝角三角形时,有两边和其中一边上的高对应相等的两个三角形不全等,故原说法错误;
③有一边对应相等的两个等腰直角三角形全等,若是腰对应相等,可以根据SAS判定全等,若是底边对应相等,由于底角都是45°,可根据ASA判定全等.故原说法正确;
④有一边重合的两个等腰三角形全等不一定全等,当一个等腰三角形的腰与另一个等腰三角形的底重合时,两者就不全等,故原说法错误;
故选C.
②两边对应相等的两个直角三角形全等,若是两条直角边对应相等,可以根据SAS判定全等,若是直角边与斜边对应相等,可根据HL判定全等.故原说法正确;
如果这两个三角形一个是锐角三角形,一个是钝角三角形时,有两边和其中一边上的高对应相等的两个三角形不全等,故原说法错误;
③有一边对应相等的两个等腰直角三角形全等,若是腰对应相等,可以根据SAS判定全等,若是底边对应相等,由于底角都是45°,可根据ASA判定全等.故原说法正确;
④有一边重合的两个等腰三角形全等不一定全等,当一个等腰三角形的腰与另一个等腰三角形的底重合时,两者就不全等,故原说法错误;
故选C.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
解方程
(
x+4)=1,下列变形中,较简单的是( )
| 3 |
| 8 |
| 8 |
| 3 |
A、方程两边同时乘8,得3(
| ||||||
B、去括号得x+
| ||||||
C、两边同时乘
| ||||||
D、括号内先通分得
|
 如图所示,两直线l1,l2交于点P,求P点的坐标.
如图所示,两直线l1,l2交于点P,求P点的坐标.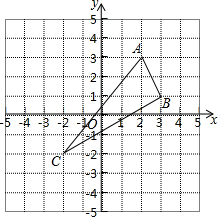 如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).