题目内容
如题1所示,在A、B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的距离y(千米)与行驶时间x(小时)之间的函数关系图象.
A,B两地相距 千米,客、货两车 小时相遇,相遇时离B地 千米.
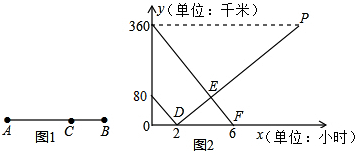
A,B两地相距

考点:一次函数的应用
专题:
分析:根据x=0时,客车与货车距离C地的距离列式计算即可得解;
先求出客车与货车的速度,再根据相遇问题列式求解即可;
根据相遇时间求出相遇时甲行驶的路程,然后求解即可.
先求出客车与货车的速度,再根据相遇问题列式求解即可;
根据相遇时间求出相遇时甲行驶的路程,然后求解即可.
解答:解:x=0时,y的值为80和360,
所以,A,B两地相距80+360=440千米,
客车的速度为:360÷6=60千米/小时,
货车的速度为:80÷2=40千米/小时,
客、货两车440÷(60+40)=4.4小时相遇,
相遇时离B地:360-60×4.4=96千米.
故答案为:440;4.4;96.
所以,A,B两地相距80+360=440千米,
客车的速度为:360÷6=60千米/小时,
货车的速度为:80÷2=40千米/小时,
客、货两车440÷(60+40)=4.4小时相遇,
相遇时离B地:360-60×4.4=96千米.
故答案为:440;4.4;96.
点评:本题考查了一次函数的应用,主要利用了时间、路程、速度三者之间的关系,准确识图理解两车的行驶过程是解题的关键.

练习册系列答案
相关题目
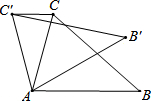 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )| A、30° | B、35° |
| C、40° | D、50° |
 如图,矩形ABCD中,AB=3,AD=5.将矩形ABCD在直线l上按顺时针方向不滑动地每秒转动90°,转动3秒后停止,则顶点A经过的路线长为
如图,矩形ABCD中,AB=3,AD=5.将矩形ABCD在直线l上按顺时针方向不滑动地每秒转动90°,转动3秒后停止,则顶点A经过的路线长为
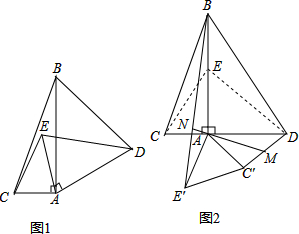
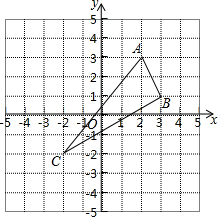 如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).