题目内容
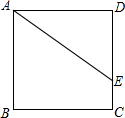如图，正方形ABCD的面积为3，点E是DC边上一点，DE=1，将线段AE绕点A旋转，使点E落在直线BC上，落点记为F，则∠EAF=考点：旋转的性质
专题：
分析：由旋转的性质可得△ADE≌△ABF，可得到BF=DE，∠DAE=∠BAF=30°，可求得答案．
解答：解：∵四边形ABCD为正方形，且面积为3
∴∠D=∠B=∠BAD=90°，AD=AB=BC=CD=
，且AE=AF，
在Rt△ADE和Rt△ABF中，
，
∴Rt△ADE≌Rt△ABF（HL），
∴∠DAE=∠BAF，BF=DE=1，
又∵在Rt△ADE中，DE=1，AD=
，
∴tan∠DAE=
，
∴∠BAF=∠DAE=30°，
∴∠EAF=90°=30°-30°=30°，FC=BC-BF=
-1，
故答案为：30°；
-1．
∴∠D=∠B=∠BAD=90°，AD=AB=BC=CD=
| 3 |
在Rt△ADE和Rt△ABF中，
|
∴Rt△ADE≌Rt△ABF（HL），
∴∠DAE=∠BAF，BF=DE=1，
又∵在Rt△ADE中，DE=1，AD=
| 3 |
∴tan∠DAE=
| ||
| 3 |
∴∠BAF=∠DAE=30°，
∴∠EAF=90°=30°-30°=30°，FC=BC-BF=
| 3 |
故答案为：30°；
| 3 |
点评：本题主要考查旋转的性质及正主形的性质，利用旋转的性质证明△ADE≌△ABF是解题的关键．
练习册系列答案
相关题目
如图，将长方形ABCD沿AE折叠，使D点落在BC边上的点F处，已知AD=10，AB=8，求EC的长．
我们把两相邻边分别相等的四边形叫做“筝形”．如图，在筝形ABCD中，AB=AD，BC=DC，AC、BD相交于点O．如果直角三角形的三条边长分别是3，4，x，那么x的值为（ ）
| A、4 | ||
| B、5 | ||
C、4或
| ||
D、5或
|
已知在△ABC中，D是AB上一点，P是AC上一点．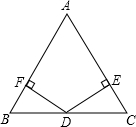
如图，在△ABC中，已知D是BC的中点，DF⊥AB于点F，DE⊥AC于点E，且DF=DE，那么AB=AC吗？你能用学过的知识完成这个问题吗？
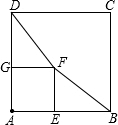已知正方形ABCD和正方形AEFG有一个公共点A，点G、E分别在线段AD、AB上．如图，连结DF、BF．