题目内容
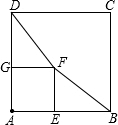 已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.如图,连结DF、BF.
已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.如图,连结DF、BF.(1)求证:DF=BF;
(2)若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明.
考点:旋转的性质,正方形的性质
专题:
分析:(1)利用正方形的性质证明△DGF≌△BEF即可;
(2)不正确,当点F落在AB上时可证明DF≠BF.
(2)不正确,当点F落在AB上时可证明DF≠BF.
解答:(1)证明:∵四边形ABCD和四边形AEFG为正方形,
∴AG=AE,AD=AB,GF=EF,∠DGF=∠BEF=90°,
∴DG=BE,
在△DGF和△BEF中,
,
∴△DGF≌△BEF(SAS),
∴DF=BF;
(2)解:不正确,
如图,当F点落在AB上时,连接DF,显然DF>AD,则DF>AB,而F在AB上,则AB>BF,

∴DF>BF,
∴不正确.
∴AG=AE,AD=AB,GF=EF,∠DGF=∠BEF=90°,
∴DG=BE,
在△DGF和△BEF中,
|
∴△DGF≌△BEF(SAS),
∴DF=BF;
(2)解:不正确,
如图,当F点落在AB上时,连接DF,显然DF>AD,则DF>AB,而F在AB上,则AB>BF,

∴DF>BF,
∴不正确.
点评:本题主要考查正方形的性质及全等三角形的判定和性质,掌握全等三角形的对应边相等是解题的关键,注意利用正方形的性质找三角形全等的条件.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
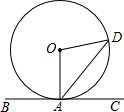 如图,直线BC与⊙O相切于点A,AD是⊙O的弦,连接OD,若∠DAC=50°,则∠ODA的度数为( )
如图,直线BC与⊙O相切于点A,AD是⊙O的弦,连接OD,若∠DAC=50°,则∠ODA的度数为( )| A、30° | B、40° |
| C、50° | D、60° |
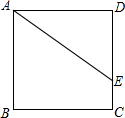 如图,正方形ABCD的面积为3,点E是DC边上一点,DE=1,将线段AE绕点A旋转,使点E落在直线BC上,落点记为F,则∠EAF=
如图,正方形ABCD的面积为3,点E是DC边上一点,DE=1,将线段AE绕点A旋转,使点E落在直线BC上,落点记为F,则∠EAF= 如图所示:若∠CDE=26°,求∠C的度数.
如图所示:若∠CDE=26°,求∠C的度数. 如图所示,∠1=∠2,BD=CD,试证明△ABC是等腰三角形.
如图所示,∠1=∠2,BD=CD,试证明△ABC是等腰三角形.