题目内容
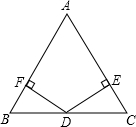 如图,在△ABC中,已知D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且DF=DE,那么AB=AC吗?你能用学过的知识完成这个问题吗?
如图,在△ABC中,已知D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且DF=DE,那么AB=AC吗?你能用学过的知识完成这个问题吗?考点:等腰三角形的判定
专题:
分析:根据点D是△ABC的BC边上的中点,DE⊥AC于E,DF⊥AB于F,且DE=DF.利用HL求证△BFD≌△DEC,可得∠B=∠C,即可证明AB=AC.
解答:解:AB=AC;
理由:∵点D是△ABC的BC边上的中点,
∴BD=DC,
∵DE⊥AC于E,DF⊥AB于F,
∴△BFD和△DEC为直角三角形,
在Rt△BFD和Rt△CED中,
,
∴Rt△BFD≌Rt△CED(HL),
∴∠B=∠C,
∴AB=AC.
理由:∵点D是△ABC的BC边上的中点,
∴BD=DC,
∵DE⊥AC于E,DF⊥AB于F,
∴△BFD和△DEC为直角三角形,
在Rt△BFD和Rt△CED中,
|
∴Rt△BFD≌Rt△CED(HL),
∴∠B=∠C,
∴AB=AC.
点评:此题主要考查学生对全等三角形的判定与性质和等腰三角形的判定与性质的理解和掌握.难度不大,属于基础题.

练习册系列答案
相关题目
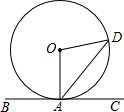 如图,直线BC与⊙O相切于点A,AD是⊙O的弦,连接OD,若∠DAC=50°,则∠ODA的度数为( )
如图,直线BC与⊙O相切于点A,AD是⊙O的弦,连接OD,若∠DAC=50°,则∠ODA的度数为( )| A、30° | B、40° |
| C、50° | D、60° |
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③a+b+c=0;④9a+3b+c<0,其中结论正确的是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③a+b+c=0;④9a+3b+c<0,其中结论正确的是 如图,在△ABC中∠BAC=62°,现将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点在同一条线上,那么旋转角的度数为
如图,在△ABC中∠BAC=62°,现将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点在同一条线上,那么旋转角的度数为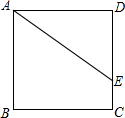 如图,正方形ABCD的面积为3,点E是DC边上一点,DE=1,将线段AE绕点A旋转,使点E落在直线BC上,落点记为F,则∠EAF=
如图,正方形ABCD的面积为3,点E是DC边上一点,DE=1,将线段AE绕点A旋转,使点E落在直线BC上,落点记为F,则∠EAF= 在正方形ABCD中,E是AD的中点,点F在DC上,且DF:FC=1:3,试判断△BEF的形状,并说明理由.
在正方形ABCD中,E是AD的中点,点F在DC上,且DF:FC=1:3,试判断△BEF的形状,并说明理由. 在平面直角坐标系中描出下列各点A(2,1),B(0,1),C(-2,3),D(4,3),并将各点用线段依次连接构成一个四边形ABCD.
在平面直角坐标系中描出下列各点A(2,1),B(0,1),C(-2,3),D(4,3),并将各点用线段依次连接构成一个四边形ABCD.