题目内容
2.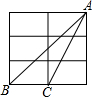 如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )
如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 根据题意可得∠D=90°,AD=3×1=3,BD=2×2=4,然后由勾股定理求得AB的长,又由余弦的定义,即可求得答案.
解答  解:如图,∵由6块长为2、宽为1的长方形,
解:如图,∵由6块长为2、宽为1的长方形,
∴∠D=90°,AD=3×1=3,BD=2×2=4,
∴在Rt△ABD中,AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=5,
∴cos∠ABC=$\frac{BD}{AB}$=$\frac{4}{5}$.
故选D.
点评 此题考查了锐角三角函数的定义以及勾股定理.此题比较简单,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C的大小是( )
如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C的大小是( )
 如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C的大小是( )
如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C的大小是( )| A. | 25° | B. | 40° | C. | 65° | D. | 115° |
17. 某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
根据图表信息,回答下列问题:
(1)该班共有学生40人;表中a=20;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
 某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:| 类别 | 成绩 | 频数 |
| 甲 | 60≤m<70 | 5 |
| 乙 | 70≤m<80 | a |
| 丙 | 80≤m<90 | 10 |
| 丁 | 90≤m≤100 | 5 |
(1)该班共有学生40人;表中a=20;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
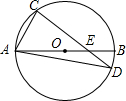 如图,AB为⊙O的直径,弦CD与AB交于点E,连接AD.若∠C=80°,∠CEA=30°,则∠CDA=20°.
如图,AB为⊙O的直径,弦CD与AB交于点E,连接AD.若∠C=80°,∠CEA=30°,则∠CDA=20°. 图中所示的几何体是由一些小立方块搭成的,则这个几何体的主视图是( )
图中所示的几何体是由一些小立方块搭成的,则这个几何体的主视图是( )



 如图,AB是圆O的直径,点C在圆O上,若∠A=40°,则∠B的度数为50°.
如图,AB是圆O的直径,点C在圆O上,若∠A=40°,则∠B的度数为50°.